Advertisements
Advertisements
प्रश्न
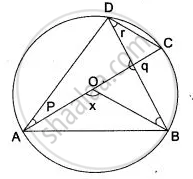
In the figure, AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q, r in term of x.
उत्तर
∠ ADB = `1/2 "∠ AOB" = x/2`
∠ ADB = 90° - r
∠ ADB = ∠ ACB = q
Combining these, we get
`x/2 = 90° - r = q`
⇒ 2r = 180° - x
and x = 2q
∠ DAC = ∠ CAB
∠ DAC = ∠ BDC
⇒ p = r = `1/2` (180° - x)
APPEARS IN
संबंधित प्रश्न
The radius of a circle is 17.0 cm and the length of perpendicular drawn from its centre to a chord is 8.0 cm. Calculate the length of the chord.
Two chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the bisector of angle BAC.
In the following figure, a circle is inscribed in the quadrilateral ABCD.

If BC = 38 cm, QB = 27 cm, DC = 25 cm and that AD is perpendicular to DC, find the radius of the circle.
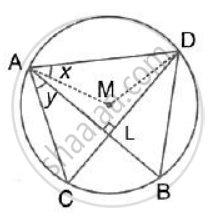
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other.
If ∠MAD = x and ∠BAC = y , Prove that : x = y
Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm;
find the length of another chord.
A chord of length 8 cm is drawn at a distance of 3 cm from the center of the circle.
Calculate the radius of the circle.
In the following figure, the line ABCD is perpendicular to PQ; where P and Q are the centers of the circles.
Show that:
(i) AB = CD ;
(ii) AC = BD.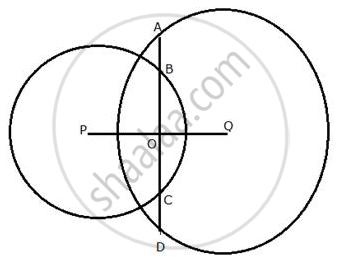
AB and CD are two parallel chords of a circle such that AB = 10 cm and CD = 24 cm. If the chords are on the opposite sides of the centre and the distance between them is 17 cm, find the radius of the circle.
In Fig. O is the centre of the circle of radius 5 cm. OP ⊥ AB, OQ ⊥ CD, AB || CD, AB = 6 cm and CD = 8 cm. Determine PQ.

In the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD.

AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the
(i) radius of the circle
(ii) length of chord CD.
