Advertisements
Advertisements
प्रश्न
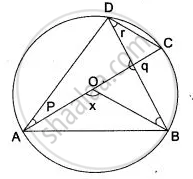
In the figure, AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q, r in term of x.
उत्तर
∠ ADB = `1/2 "∠ AOB" = x/2`
∠ ADB = 90° - r
∠ ADB = ∠ ACB = q
Combining these, we get
`x/2 = 90° - r = q`
⇒ 2r = 180° - x
and x = 2q
∠ DAC = ∠ CAB
∠ DAC = ∠ BDC
⇒ p = r = `1/2` (180° - x)
APPEARS IN
संबंधित प्रश्न
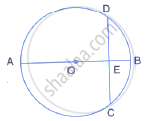
The figure given below, shows a circle with centre O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4cm, find the radius of the circle.
The given figure shows two circles with centres A and B; and radii 5 cm and 3 cm respectively, touching each other internally. If the perpendicular bisector of AB meets the bigger circle in P and Q, find the length of PQ.

Two chords of lengths 10cm and 24cm are drawn parallel o each other in a circle. If they are on the same side of the centre and the distance between them is 17cm, find the radius of the circle.
From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
OP is the ⊥ bisector of chord AB.
In the given figure, O is the center of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm, 
Find the :
(i) the radius of the circle
(ii) length of chord CD.
The radius of a circle is 17.0 cm and the length of the perpendicular drawn from its center to a chord is 8.0 cm.
Calculate the length of the chord.
In the following figure, AD is a straight line, OP ⊥ AD and O is the centre of both circles. If OA = 34cm, OB = 20 cm and OP = 16 cm;
find the length of AB.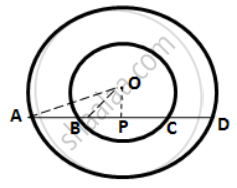
AB and CD are two equal chords of a circle with center O which intersect each other at a right angle at point P.
If OM ⊥ AB and ON ⊥ CD;
show that OMPN is a square.
Find the length of a chord which is at a distance of 5 cm from the centre of a circle of radius 13 cm.
In Fig. O is the centre of the circle of radius 5 cm. OP ⊥ AB, OQ ⊥ CD, AB || CD, AB = 6 cm and CD = 8 cm. Determine PQ.

