Advertisements
Advertisements
प्रश्न
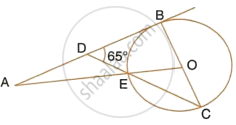
In the adjoining figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
उत्तर १
AB is a straight line.
∴ ∠ADE + ∠BDE = 180°
`=>` ∠ADE + 65° = 180°
`=>` ∠ADE = 115° ...(i)
AB i.e. DB is tangent to the circle at point B and BC is the diameter.
∴ ∠DB = 90°
In ΔBDC,
∠DBC + ∠BDC + ∠DCB = 180°
`=>` 90° + 65° + ∠DCB = 180°
`=>` ∠DCB = 25°
Now, OE = OC ...(Radii of the same circle)
∴ ∠DCB or ∠OCE = ∠OEC = 25°
Also,
∠OEC = ∠DEC = 25° ...(Vertically opposite angles)
In ΔADE,
∠ADE + ∠DEA + ∠DAE = 180°
From (i) and (ii)
115° + 25° + ∠DAE = 180°
`=>` ∠DAE or ∠BAO = 180° – 140° = 40°
∴ ∠BAO = 40°
उत्तर २
As AB is a tangent to the circle at B and OB is radius, OB + AB `=>` ∠CBD = 90°.
In ΔBCD,
∠BCD + ∠CBD + ∠BDC = 180°
∠BCD + 90° + 65° = 180°
∠BCD + 155° = 180°
∠BCD = 180° – 155°
∠BCD = 25°
∠BOE = 2∠BCE ...(Angle at centre = double the angle at the remaining part of circle)
∠BOE = 2 × 25°
∠BOE = 50°
∠BOA = 50°
In ΔBOA,
∠BAO + ∠ABO + ∠BOA = 180°
∠BAO + 90° + 50° = 180°
∠BAO + 140° = 180°
∠BAO = 180° – 140°
∠BAO = 40°
संबंधित प्रश्न
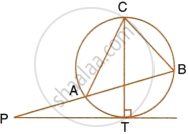
PT is a tangent to the circle at T. If ∠ABC = 70° and ∠ACB = 50°; calculate:
- ∠CBT
- ∠BAT
- ∠APT
In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that:
`∠CAD = 1/2 (∠PBA - ∠PAB)`

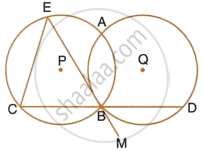
Circles with centres P and Q intersect at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circle are congruent; show that CE = BD.
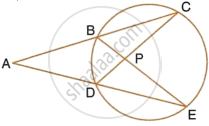
In the given figure, AC = AE. Show that:
- CP = EP
- BP = DP
In the given figure, XY is the diameter of the circle and PQ is a tangent to the circle at Y.
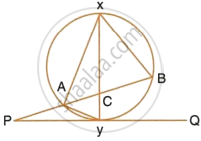
If ∠AXB = 50° and ∠ABX = 70°, find ∠BAY and ∠APY.
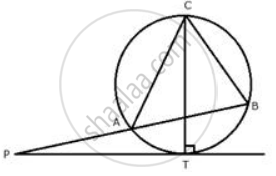
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT

PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT
A circle touches the sides of a quadrilateral ABCD at P, Q, R, S respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.
A, B, and C are three points on a circle. The tangent at C meets BN produced at T. Given that ∠ ATC = 36° and ∠ ACT = 48°, calculate the angle subtended by AB at the center of the circle.
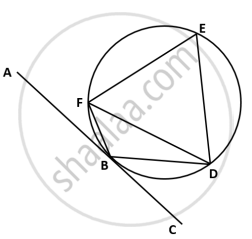
In the given figure, AC is a tangent to circle at point B. ∆EFD is an equilateral triangle and ∠CBD = 40°. Find:
- ∠BFD
- ∠FBD
- ∠ABF
