Advertisements
Advertisements
प्रश्न
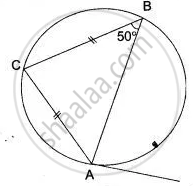
In the given figure, XY is the diameter of the circle and PQ is a tangent to the circle at Y.
If ∠AXB = 50° and ∠ABX = 70°, find ∠BAY and ∠APY.
उत्तर
In the above figure,
XY is a diameter of the circle PQ is tangent to the circle at Y.
∠AXB = 50° and ∠ABX = 70°
i. In ΔAXB,
∠XAB + ∠ABX + ∠AXB = 180° ...(Angles of a triangle)
`=>` ∠XAB + 70° + 50° = 180°
`=>` ∠XAB + 120° = 180°
`=>` ∠XAB = 180° – 120° = 60°
But, ∠XAY = 90° ...(Angle in a semicircle)
∴ ∠BAY = ∠XAY – ∠XAB
= 90° – 60°
= 30°
ii. Similarly ∠XBY = 90° ...(Angle in a semicircle)
And ∠CXB = 70°
∴ ∠PBY = ∠XBY – ∠XBA
= 90° – 70°
= 20°
∴ ∠BYA = 180° – ∠AXB ...(∵ ∠BYA + ∠AYB = 180°)
= 180° – 50°
= 130°
∠PYA = ∠ABY ...(Angles in the alternate segment)
∠PBY = 20°
And ∠PYB = ∠PYA + ∠AYB
= 20° + 130°
= 150°
∴ ∠APY = 180° – (∠PYA + ∠ABY)
= 180° – (150° + 20°)
= 180° – 170°
= 10°
APPEARS IN
संबंधित प्रश्न
Two circle touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
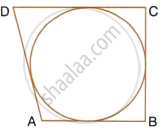
If the sides of a parallelogram touch a circle in following figure, prove that the parallelogram is a rhombus.
From the given figure, prove that : AP + BQ + CR = BP + CQ + AR.
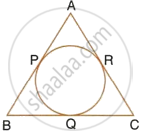
Also show that : AP + BQ + CR = `1/2` × Perimeter of ΔABC.
From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
∠AOP = ∠BOP
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate :
- ∠QOR
- ∠QPR;
given that ∠A = 60°.
In the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P. Given ∠SPR = x° and ∠QRP = y°;
Prove that:
- ∠ORS = y°
- write an expression connecting x and y.

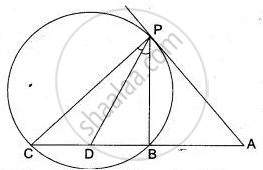
In Fig. AP is a tangent to the circle at P, ABC is secant and PD is the bisector of ∠BPC. Prove that ∠BPD = `1/2` (∠ABP - ∠APB).
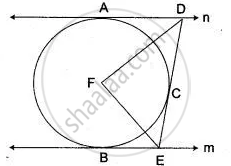
In Fig. l and m are two parallel tangents at A and B. The tangent at C makes an intercept DE between n and m. Prove that ∠ DFE = 90°
In the Figure, PT is a tangent to a circle. If m(∠BTA) = 45° and m(∠PTB) = 70°. Find m(∠ABT).

In Fig. AT is a tangent to the circle. If m∠ABC = 50°, AC = BC, Find ∠BAT.