Advertisements
Advertisements
प्रश्न
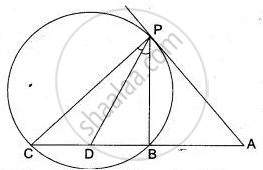
In Fig. AP is a tangent to the circle at P, ABC is secant and PD is the bisector of ∠BPC. Prove that ∠BPD = `1/2` (∠ABP - ∠APB).
उत्तर
Since ∠APB and ∠BCP are angles in the alternate segment of chord PB.
∴ ∠APB = ∠BCP ...(i)
Since PD is the bisector of ∠BPC.
∴ ∠CPB = 2 ∠BPD ...(ii)
In ΔPCB, side CB has been produced to A, forming exterior angle ∠ABP.
∴ ∠ABP = ∠BCP + ∠CPB
⇒ ∠ABP = ∠APB + 2 ∠BPD ....(Using (i) and (ii))
⇒ 2 ∠BPD = ∠ABP - ∠APB
⇒ ∠BPD = `1/2`(∠ABP - ∠APB)
Hence proved.
APPEARS IN
संबंधित प्रश्न
From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
∠AOP = ∠BOP
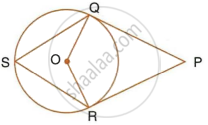
In the following figure, PQ and PR are tangents to the circle, with centre O. If `∠`QPR = 60°, calculate:
- ∠QOR,
- ∠OQR,
- ∠QSR.
If PQ is a tangent to the circle at R; calculate:
- ∠PRS,
- ∠ROT.
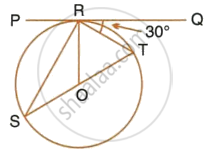
Given O is the centre of the circle and angle TRQ = 30°.
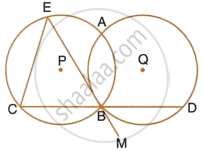
Circles with centres P and Q intersect at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circle are congruent; show that CE = BD.
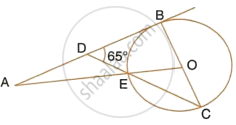
In the adjoining figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
ABC is a right triangle with angle B = 90°, A circle with BC as diameter meets hypotenuse AC at point D. Prove that: AC × AD = AB2
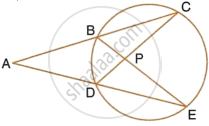
In the given figure, AC = AE. Show that:
- CP = EP
- BP = DP
A circle touches the sides of a quadrilateral ABCD at P, Q, R, S respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.
A, B, and C are three points on a circle. The tangent at C meets BN produced at T. Given that ∠ ATC = 36° and ∠ ACT = 48°, calculate the angle subtended by AB at the center of the circle.
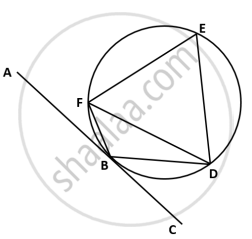
In the given figure, AC is a tangent to circle at point B. ∆EFD is an equilateral triangle and ∠CBD = 40°. Find:
- ∠BFD
- ∠FBD
- ∠ABF
