Advertisements
Advertisements
प्रश्न
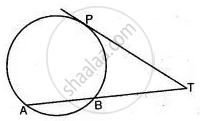
In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

उत्तर
In order to prove that ΔADT is isosceles i.e., TA = TD, it is sufficient to show that ∠TAD = ∠TDA.
Since ∠TAB and ∠BCA are angles in the alternate segments of chord AB.
∴ ∠TAB = ∠BCA ...(i)
It is given that AD is the bisector of ∠BAC.
∠BAD = ∠CAD ...(ii)
Now, ∠TAD = ∠TAB + ∠BAD
⇒ ∠TAD = ∠BCA + ∠CAD ....(Using (i) and (ii))
⇒ ∠TAD = ∠DCA + ∠CAD ....( ∵∠BCA = ∠DCA)
⇒ ∠TAD = 180° - ∠CAD ....( In ΔCAD, ∠CAD + ∠DCA +∠CDA = 180° ∴ ∠CAD + ∠BCA = 180° - ∠CAD)
⇒ ∠TAD = ∠TDA ....(∵∠CDA + ∠TDA = 180°)
= TD = TA
Hence, ΔADT is isosceles
Hence proved.
APPEARS IN
संबंधित प्रश्न
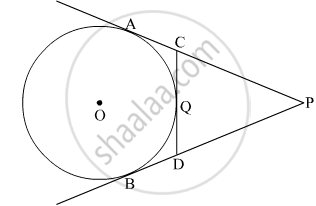
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD
From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ∠ BAM = ∠ BMA
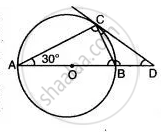
In Figure, AB is diameter and AC is a chord of a circle such that ∠BAC = 30°. The tangent at C intersects AB produced at D. Prove that BC = BD.
In Fig. the incircle of ΔABC touches the sides BC, CA, and AB at D, E respectively. Show that: AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)

In the figure given below, PT is a tangent to the circle. Find PT if AT = 16 cm and AB = 12 cm.
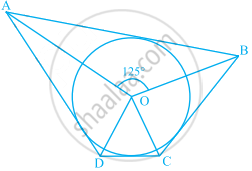
In figure, if ∠AOB = 125°, then ∠COD is equal to ______.
In figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to ______.

The quadrilateral formed by joining the angle bisectors of a cyclic quadrilateral is a ______
A tangent JK is drawn to a circle with centre C such that CK = 6 cm and ∠CKJ = 60°. Find the length of the tangent JK.

