Advertisements
Advertisements
प्रश्न
From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is
पर्याय
A. 25
B. `sqrt313`
C. 5
D. 1
उत्तर
The given information can be represented diagrammatically as follows:

Let O be the centre of the circle.
Given: PQ = 12 cm and OQ = 13 cm.
To find: Radius of the circle
PQ is a tangent drawn from the external point Q to the circle.
∠ OPQ = 90° (Radius is perpendicular to the tangent at the point of contact)
On applying Pythagoras theorem in ΔOPQ, we obtain:
OQ2 = OP2 + PQ2
∴ OP2 = OQ2 − PQ2
⇒ OP2 = (13 cm)2 − (12 cm)2
⇒ OP2 = 169cm2 − 144 cm2
⇒ OP2 = 25 cm2
⇒ OP = 5 cm
Thus, the radius of circle is 5 cm.
Hence, the correct answer is C
APPEARS IN
संबंधित प्रश्न
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
What is the distance between two parallel tangents of a circle having radius 4.5 cm ? Justify your answer.
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find AB.

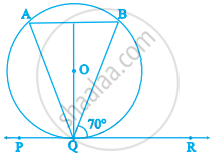
In figure, if PQR is the tangent to a circle at Q whose centre is O, AB is a chord parallel to PR and ∠BQR = 70°, then ∠AQB is equal to ______.
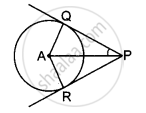
In the figure, PQ and PR are tangents to a circle with centre A. If ∠QPA=27°, then ∠QAR equals to ______
ABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ = 65°, then ∠BCD is ______

In Question 5 above, if radii of the two circles are equal, prove that AB = CD.
Construct a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
In the given figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 25°, then x is equal to ______.

