Advertisements
Advertisements
प्रश्न
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
उत्तर १
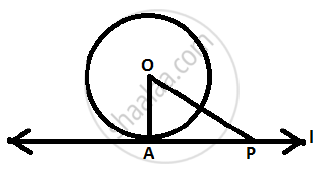
Given: Line is tangent to the (O, r) at point A.
To prove: `bar(OA) _|_ l`
Proof: Let P ∈ l , P ≠ A.
If P is in the interior of (O,r), then the line will be a secant of the circle and not a tangent.
But l is a tangent of the circle, so P is not in the interior of the circle.
Also P≠A
P is the point in the exterior of the circle.
OP > OA ( `bar(OA)` is the radius of the circle )
Therefore each point P ∈ l except A satisfies the inequality OP > OA.
Therefore OA is the shortest distance of line l from O.
`bar(OA) _|_ l`
उत्तर २

Given: A circle C (0, r) and a tangent l at point A
To prove: OA ⊥ l
Construction:
Take a point B, other than A, on the tangent l. Join OB. Suppose OB meets the circle in C.
Proof: We know that among all line segments joining the point O to a point on l, the perpendicular is shortest to l.
OA = OC (Radius of the same circle)
Now,
OB = OC + BC
⇒ OB > OC
⇒ OB > OA
⇒ OA < OB
B is an arbitrary point on the tangent l. Thus, OA is shorter than any other line segment joining O to any point on l.
Here,
OA ⊥ l
Hence, the tangent at any point of a circle is perpendicular to the radius through the point of contact.
APPEARS IN
संबंधित प्रश्न
Draw a circle of radius 3.5 cm. Marks a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
In the following figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

Four alternative answers for the following question is given. Choose the correct alternative.
If two circles are touching externally, how many common tangents of them can be drawn?
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
In fig., AB and DC are two chords of a circle with centre O. these chords when produced meet at P. if PB = Bern, BA = 7cm and PO = 14.5cm, find the radius of the circle.
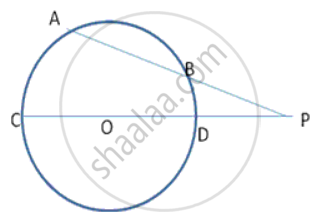
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
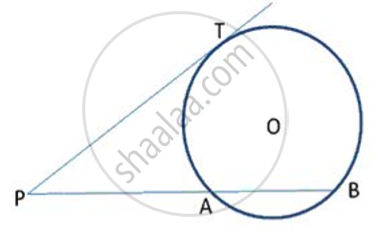
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate : ∠CDB

In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ∠ BAM = ∠ BMA
