Advertisements
Advertisements
प्रश्न
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
उत्तर १
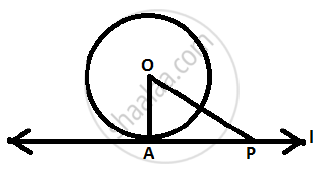
Given: Line is tangent to the (O, r) at point A.
To prove: `bar(OA) _|_ l`
Proof: Let P ∈ l , P ≠ A.
If P is in the interior of (O,r), then the line will be a secant of the circle and not a tangent.
But l is a tangent of the circle, so P is not in the interior of the circle.
Also P≠A
P is the point in the exterior of the circle.
OP > OA ( `bar(OA)` is the radius of the circle )
Therefore each point P ∈ l except A satisfies the inequality OP > OA.
Therefore OA is the shortest distance of line l from O.
`bar(OA) _|_ l`
उत्तर २

Given: A circle C (0, r) and a tangent l at point A
To prove: OA ⊥ l
Construction:
Take a point B, other than A, on the tangent l. Join OB. Suppose OB meets the circle in C.
Proof: We know that among all line segments joining the point O to a point on l, the perpendicular is shortest to l.
OA = OC (Radius of the same circle)
Now,
OB = OC + BC
⇒ OB > OC
⇒ OB > OA
⇒ OA < OB
B is an arbitrary point on the tangent l. Thus, OA is shorter than any other line segment joining O to any point on l.
Here,
OA ⊥ l
Hence, the tangent at any point of a circle is perpendicular to the radius through the point of contact.
APPEARS IN
संबंधित प्रश्न
If the angle between two tangents drawn from an external point P to a circle of radius a and centre O, is 60°, then find the length of OP
In Figure 1, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC
= 4 cm, then the length of AP (in cm) is
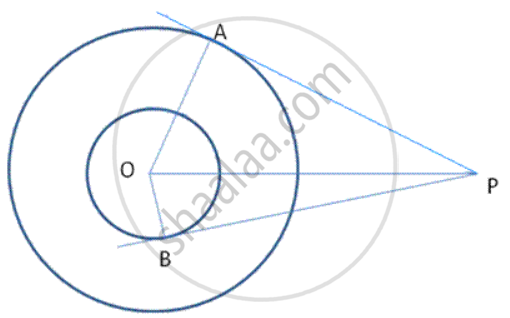
Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
A point A is 17cm from the centre of the circle. The length of the tangent drawn from A to the circle is 15cm. find the radius of the circle.
In followinf fig., two concentric circles with centre 0 are of radii 5 cm and 3 cm. from an external point P, tangents PA and PB are drawn to these circles. If AP = 12cm, find BP.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate ∠ PAD.

In Figure, AB is diameter and AC is a chord of a circle such that ∠BAC = 30°. The tangent at C intersects AB produced at D. Prove that BC = BD.
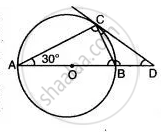
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
- AB.
- the length of tangent PT.
The length of tangent drawn to a circle of radius 9 cm from a point 41 cm from the centre is ______.
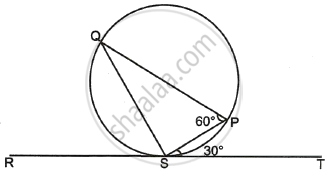
In the given diagram RT is a tangent touching the circle at S. If ∠PST = 30° and ∠SPQ = 60°, then ∠PSQ is equal to ______.