Advertisements
Advertisements
प्रश्न
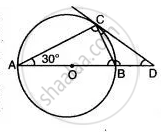
In Figure, AB is diameter and AC is a chord of a circle such that ∠BAC = 30°. The tangent at C intersects AB produced at D. Prove that BC = BD.
उत्तर
Join OC.
∠ ACB = 90° ...(Angle of the semicircle)
∠ ABC = 60° ...(Angle Sum property)
∠ CBD = 120° ...(adj to angle CBA 30°)
∠ OCD = 90° ...(tangent)
∠ COB = 60° ...(Angle at the center is equal to twice that of the circumference)
∠ OCB = 60° ...(Angle Sum property)
∠BCD = ∠ OCD - ∠OCB = 90° - 60° = 30°
∠BDC = ∠BCD = 30°
BD = BC
Hence proved.
APPEARS IN
संबंधित प्रश्न
The common point of a tangent to a circle and the circle is called ______.
In the given figure O is the centre of the circle. Tangents A and B meet at C. If ∠ACO = 30°, find
1) ∠BCO
2) ∠AOB
3) ∠APB
In Figure 5, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of ΔPQR = 189 cm2, then find the lengths of sides PQ and PR.
A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
In following fig., PT is tangent to the circle at T and CD is a diameter of the same circle. If PC= 3cm and PT= 6cm, find the radius of the circle.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate ∠ PAD.

In the following figure, PA and PB are tangents from a point P to a circle with centre O. Then the quadrilateral OAPB must be a ______


In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
In the given figure, XAY is a tangent to the circle centered at O. If ∠ABO = 40°, then find ∠BAY and ∠AOB.

If O is centre of a circle and Chord PQ makes an angle 50° with the tangent PR at the point of contact P, then the angle subtended by the chord at the centre is ______.