Advertisements
Advertisements
प्रश्न
In Figure 5, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of ΔPQR = 189 cm2, then find the lengths of sides PQ and PR.
उत्तर
Let PQ and PR touch the circle at points S and U respectively. Join O with P, Q, R, S and U.
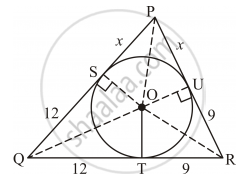
We have, OS = OT = OU = 6 cm (Radii of the circle)
QT = 12 cm and TR = 9 cm
∴ QR = QT + TR = 12 cm + 9 cm = 21 cm
Now, QT = QS = 12 cm (Tangents from the same point)
TR = RU = 9 cm
Let PS = PU = x cm
Then, PQ = PS + SQ = (12 + x) cm and PR = PU + RU = (9 + x) cm
It is clear that
ar (ΔOQR) + ar (ΔOPR) + ar (ΔOPQ) = ar (ΔPQR)
`rArr 1/2xxQRxxOT+1/2xxPRxxOU+1/2xxPQxxOS=189` `(given : ar(Δ PQR)=189cm^2)`
`rArr 1/2xx21xx6+1/2xx(9+x)xx6+1/2xx(12+x)xx6=189`
`rArr 1/2xx6(21+9+x+12+x)=189`
⇒ 3 (42 + 2x) = 189
⇒ 42 + 2x = 63
⇒ 2x = 21
⇒ x = 10.5
Thus, PQ = (12 + 10.5) cm = 22.5 cm and PR = (9 + 10.5) cm = 19.5 cm.
APPEARS IN
संबंधित प्रश्न
In the given figure O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of a circle.

In the following figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
In Figure 3, a right triangle ABC, circumscribes a circle of radius r. If AB and BC are of lengths of 8 cm and 6 cm respectively, find the value of r.

What is the distance between two parallel tangents of a circle having radius 4.5 cm ? Justify your answer.
ABC is a right triangle with angle B = 90º. A circle with BC as diameter meets by hypotenuse AC at point D. Prove that: BD2 = AD × DC.
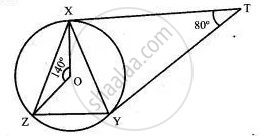
In the alongside, figure, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°. Calculate the value of ∠ZXY.
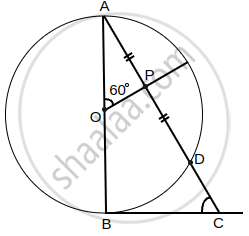
In the given figure, AB is diameter of a circle centered at O. BC is tangent to the circle at B. If OP bisects the chord AD and ∠AOP = 60°, then find ∠C.
In the given figure, XAY is a tangent to the circle centered at O. If ∠ABO = 40°, then find ∠BAY and ∠AOB.

In the given figure, PQ is a tangent to the circle with centre O. If ∠OPQ = x, ∠POQ = y, then x + y is ______.
Assertion (A): A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R): The lengths of tangents drawn from an external point to a circle are equal.
