Advertisements
Advertisements
प्रश्न
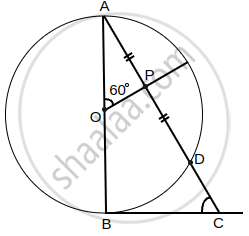
In the given figure, AB is diameter of a circle centered at O. BC is tangent to the circle at B. If OP bisects the chord AD and ∠AOP = 60°, then find ∠C.
उत्तर

Since, OP bisects the chord AD, therefore ∠OPA = 90° ....[∵ The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord]
Now, In ΔAOP,
∠A = 180° – 60° – 90°
= 120° – 90°
= 30°
Also, we know that the tangent at any point of a circle is perpendicular to the radius through the point of contact
∴ ∠ABC = 90°
Now, In ΔABC,
∠C = 180° – ∠A – ∠B
= 180° – 30° – 90°
= 150° – 90°
= 60°
APPEARS IN
संबंधित प्रश्न
The common point of a tangent to a circle and the circle is called ______.
In Figure 3, a right triangle ABC, circumscribes a circle of radius r. If AB and BC are of lengths of 8 cm and 6 cm respectively, find the value of r.

Four alternative answers for the following question is given. Choose the correct alternative.
If two circles are touching externally, how many common tangents of them can be drawn?
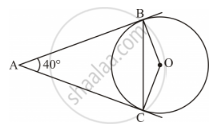
In the given Figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°. Then ∠BOC is equal to ______
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find the length of tangent PT.

Two circle with radii r1 and r2 touch each other externally. Let r be the radius of a circle which touches these two circle as well as a common tangent to the two circles, Prove that: `1/sqrtr + 1/sqrtr_1 + 1/sqrtr_2`.
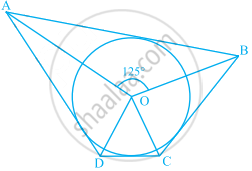
In figure, if ∠AOB = 125°, then ∠COD is equal to ______.
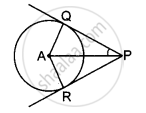
In the figure, PQ and PR are tangents to a circle with centre A. If ∠QPA=27°, then ∠QAR equals to ______
A circle of radius 5.2 cm has two tangents AB and CD parallel to each other. What is the distance between the two tangents?
