Advertisements
Advertisements
Question
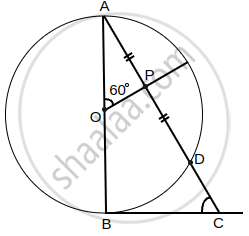
In the given figure, AB is diameter of a circle centered at O. BC is tangent to the circle at B. If OP bisects the chord AD and ∠AOP = 60°, then find ∠C.
Solution

Since, OP bisects the chord AD, therefore ∠OPA = 90° ....[∵ The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord]
Now, In ΔAOP,
∠A = 180° – 60° – 90°
= 120° – 90°
= 30°
Also, we know that the tangent at any point of a circle is perpendicular to the radius through the point of contact
∴ ∠ABC = 90°
Now, In ΔABC,
∠C = 180° – ∠A – ∠B
= 180° – 30° – 90°
= 150° – 90°
= 60°
APPEARS IN
RELATED QUESTIONS
In the figure given below, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT = 60°, find ∠PRQ.

In the given figure O is the centre of the circle. Tangents A and B meet at C. If ∠ACO = 30°, find
1) ∠BCO
2) ∠AOB
3) ∠APB
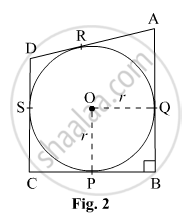
In Fig.2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5 cm, then the radius of the circle (in cm.) is:
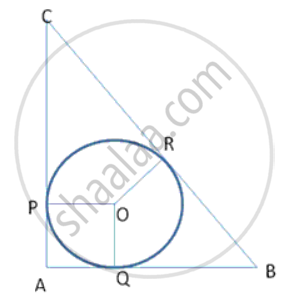
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
In following fig., ABC is a right- angled triangle at A with sides AB = 5 cm and BC = 13 cm . A circle with centre O has been inscribed in the triangle ABC. Calculate the radius of the incircle.
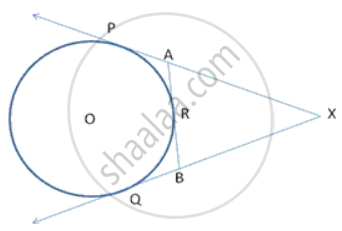
In the figure, XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that XA + AR = XB + BR.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate : ∠CDB

Construct a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.

In the given figure, QR is a common tangent to the two given circles touching externally at A. The tangent at A meets QR at P. If AP = 4.2 cm, then the length of QR is ______.
In the given diagram an isosceles ΔABC is inscribed in a circle with centre O. PQ is a tangent to the circle at C. OM is perpendicular to chord AC and ∠COM = 65°.

Find:
- ∠ABC
- ∠BAC
- ∠BCQ
