Advertisements
Advertisements
Question
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate : ∠CDB

Solution
BD is the diameter.
∴ ∠ BCD = 90° (angle in a semi – circle)
Now in ΔBCD,
∠ CDB + ∠ CBD + ∠ BCD =180°
⇒ ∠ CDB + 60° + 90° =180°
⇒ ∠ CDB =180° - 150° = 30°
APPEARS IN
RELATED QUESTIONS
A tangent to a circle intersects it in ______ point (s).
A chord of a length 16.8 cm is at a distance of 11.2 cm from the centre of a circle . Find the length of the chord of the same circle which is at a distance of 8.4 cm from the centre.
The length of the direct common tangent to two circles of radii 12cm and 4cm is 15cm. calculate the distance between their centres.
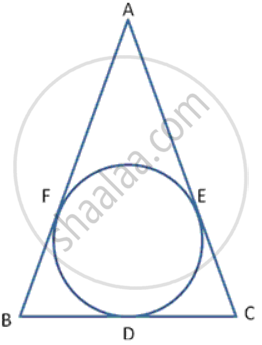
In following figure , the incircle of Δ ABC , touches the sides BC , CA and AB at D , E and F respectively. Show AF + BD + CE = AE + BF + CD
ABC is a right triangle with angle B = 90º. A circle with BC as diameter meets by hypotenuse AC at point D. Prove that: BD2 = AD × DC.
If PA and PB are two tangents drawn from a point P to a circle with center C touching it A and B, prove that CP is the perpendicular bisector of AB.
In Fig. the incircle of ΔABC touches the sides BC, CA, and AB at D, E respectively. Show that: AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)

Draw a circle of radius 2.7 cm and draw a chord PQ of length 4.5 cm. Draw tangents at points P and Q without using centre.
In the adjoining figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 30°, find the value of x.

If O is centre of a circle and Chord PQ makes an angle 50° with the tangent PR at the point of contact P, then the angle subtended by the chord at the centre is ______.