Advertisements
Advertisements
Question
In the adjoining figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 30°, find the value of x.

Solution
Given that,
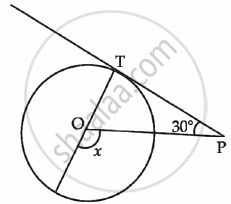
PT is a tangent at T to circle
Also, ∠TPO = 30°
So, TPO is right-angled triangle with ∠T = 90°
We have, ∠POT = (180°) – (30° + 90°) = 60°
As, x + ∠POT = 180° (linear pair angles)
`\implies` x = 180° – 120° = 60°
APPEARS IN
RELATED QUESTIONS
In Fig. 1, PQ is a tangent at a point C to a circle with centre O. if AB is a diameter and ∠CAB = 30°, find ∠PCA.

In the given figure O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of a circle.

In triangle PQR, PQ = 24 cm, QR = –7 cm and ∠PQR = 90°. Find the radius of the inscribed circle.

In fig. 5 is a chord AB of a circle, with centre O and radius 10 cm, that subtends a right angle at the centre of the circle. Find the area of the minor segment AQBP. Hence find the area of major segment ALBQA. (use π = 3.14)


In the figure, point Q is the
point of contact. If PQ = 12,
PR = 8 then find PS.
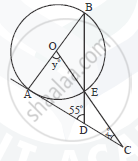
In the given figure AC is a tangent to the circle with centre O.
If ∠ADB = 55° , find x and y. Give reasons for your answers.
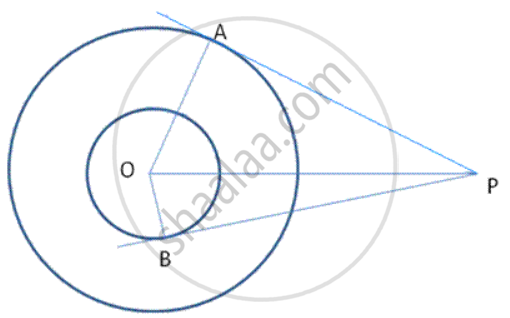
In followinf fig., two concentric circles with centre 0 are of radii 5 cm and 3 cm. from an external point P, tangents PA and PB are drawn to these circles. If AP = 12cm, find BP.
If PA and PB are two tangents drawn from a point P to a circle with center C touching it A and B, prove that CP is the perpendicular bisector of AB.
Two equal chords AB and CD of a circle with center O, when produced meet at a point E, as shown in Fig. Prove that BE = DE and AE = CE.

A: What is a line called, if it meets the circle at only one point?
B: Collection of all points equidistant from a fixed point is ______.
- Chord
- Tangent
- Circle
- Curve
- Secant
Which is correct matching?
