Advertisements
Advertisements
Question
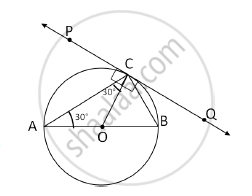
In Fig. 1, PQ is a tangent at a point C to a circle with centre O. if AB is a diameter and ∠CAB = 30°, find ∠PCA.

Solution
In the given figure,
In ΔACO,
OA = OC …(Radii of the same circle)
∴ΔACO is an isosceles triangle.
∠CAB = 30° …(Given)
∴∠CAO = ∠ACO = 30°
…(angles opposite to equal sides of an isosceles triangle are equal)
∠PCO = 90° …(radius drawn at the point of contact is perpendicular to the tangent)
Now ∠PCA = ∠PCO – ∠CAO
∴∠PCA = 90° – 30° = 60°
APPEARS IN
RELATED QUESTIONS
A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find the length of tangent PT.

ABC is a right triangle with angle B = 90º. A circle with BC as diameter meets by hypotenuse AC at point D. Prove that: BD2 = AD × DC.
Two equal chords AB and CD of a circle with center O, when produced meet at a point E, as shown in Fig. Prove that BE = DE and AE = CE.

In the figure given below, PT is a tangent to the circle. Find PT if AT = 16 cm and AB = 12 cm.
Draw a circle of radius 2.7 cm and draw a chord PQ of length 4.5 cm. Draw tangents at points P and Q without using centre.
Find the value of ∠DCE.

In the adjoining figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 30°, find the value of x.

In the given figure O, is the centre of the circle. CE is a tangent to the circle at A. If ∠ABD = 26° find:
- ∠BDA
- ∠BAD
- ∠CAD
- ∠ODB

