Advertisements
Advertisements
Question
Two equal chords AB and CD of a circle with center O, when produced meet at a point E, as shown in Fig. Prove that BE = DE and AE = CE.

Solution
Given: Two equal chords AB and CD intersecting at a point E.
To prove: BE = BE and AE = CE
Construction: Join OE. Draw OL ⊥ AB and OM ⊥ CD'
Proof: We have
AB = CD
⇒ OL = OM ....(∵Equal chords are equidistant from the centre)
In triangles OLE and OME, we have
OL = OM
∠OLE = ∠OME ...(Each equal to 90°)
and OE = OE ...(Common)
So, by SAS-Criterion of congruences
Δ OLE ≅ ΔOME
⇒ LE = ME ....(i)
Now, AB = CD
⇒ `1/2"AB" = 1/2"CD"` ⇒ BL = DM ...(ii)
Subtracting (ii) from (i), we get
LE - BL = ME - DM
⇒ BE = DE
Again, AB = CD and BE = DE
⇒ AB + BE = CD + DE
⇒ AE = CE
Hence, BE = DE and AE = CE.
Hence proved.
APPEARS IN
RELATED QUESTIONS
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is ______.
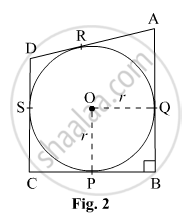
In Fig.2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5 cm, then the radius of the circle (in cm.) is:
From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is
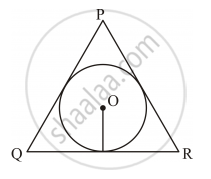
In Figure 5, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of ΔPQR = 189 cm2, then find the lengths of sides PQ and PR.
A point A is 17cm from the centre of the circle. The length of the tangent drawn from A to the circle is 15cm. find the radius of the circle.
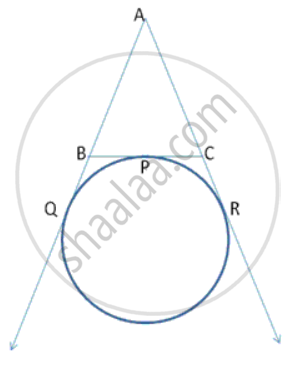
In following fig., a circle is touching the side BC of Δ ABC at P and AB and AC produced at Q and R respectively. Prove that AQ is half the perimeter of Δ ABC.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find the length of tangent PT.

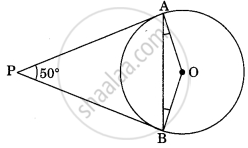
In the figure, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to ______.
In the given figure, XAY is a tangent to the circle centered at O. If ∠ABO = 40°, then find ∠BAY and ∠AOB.

A circle of radius 5.2 cm has two tangents AB and CD parallel to each other. What is the distance between the two tangents?
