Advertisements
Advertisements
प्रश्न
Two equal chords AB and CD of a circle with center O, when produced meet at a point E, as shown in Fig. Prove that BE = DE and AE = CE.

उत्तर
Given: Two equal chords AB and CD intersecting at a point E.
To prove: BE = BE and AE = CE
Construction: Join OE. Draw OL ⊥ AB and OM ⊥ CD'
Proof: We have
AB = CD
⇒ OL = OM ....(∵Equal chords are equidistant from the centre)
In triangles OLE and OME, we have
OL = OM
∠OLE = ∠OME ...(Each equal to 90°)
and OE = OE ...(Common)
So, by SAS-Criterion of congruences
Δ OLE ≅ ΔOME
⇒ LE = ME ....(i)
Now, AB = CD
⇒ `1/2"AB" = 1/2"CD"` ⇒ BL = DM ...(ii)
Subtracting (ii) from (i), we get
LE - BL = ME - DM
⇒ BE = DE
Again, AB = CD and BE = DE
⇒ AB + BE = CD + DE
⇒ AE = CE
Hence, BE = DE and AE = CE.
Hence proved.
APPEARS IN
संबंधित प्रश्न
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
In Fig. 1, AOB is a diameter of a circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, the find ∠ACO.

In the adjoining figure the radius of a circle with centre C is 6 cm, line AB is a tangent at A. Answer the following questions.
(1) What is the measure of ∠CAB ? Why ?
(2) What is the distance of point C from line AB? Why ?
(3) d(A,B) = 6 cm, find d(B,C).
(4) What is the measure of ∠ABC ? Why ? 
How many common tangents can be drawn to two circles, touching each
other externally?
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle AOB

In the following figure, seg AB is the diameter of the circle with center P. Line CB be the tangent and line AC intersects a circle in point D. Prove that:
AC x AD = 4 (radius)2

In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

The length of tangent drawn to a circle of radius 9 cm from a point 41 cm from the centre is ______.
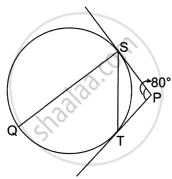
In the given diagram, PS and PT are the tangents to the circle. SQ || PT and ∠SPT = 80°. The value of ∠QST is ______.