Advertisements
Advertisements
प्रश्न
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle AOB

उत्तर
In the given fig, O is the centre of the circle and CA and CB are the tangents to the circle from C. Also, ∠ ACO = 30
P is any point on the circle. P and PB are joined.
To find : ∠AOB
Proof :
∴ ∠ ACB = 30° + 30° = 60°
∴∠ AOB + `∠`ACB = 180°
⇒ ∠ AOB + 60° = 180°
⇒ ∠ AOB = 180° - 60°
⇒ ∠ AOB = 120°
APPEARS IN
संबंधित प्रश्न
If the angle between two tangents drawn from an external point P to a circle of radius a and centre O, is 60°, then find the length of OP
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is
PA and PB are tangents from P to the circle with centre O. At M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ALOB is a cyclic quadrilateral.
Find the area of sector whose central angle and radius are 60o and 21 cm respectively.
`(pi = 22/7)`
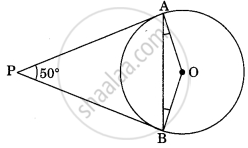
In the figure, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to ______.
ΔABC circumscribes a circle of radius r such that ∠B = 90°. If AB = 3 cm and BC = 4 cm, then find the value of r.
In the given figure, PA is a tangent to the circle drawn from the external point P and PBC is the secant to the circle with BC as diameter. If ∠AOC = 130°, then find the measure of ∠APB, where O is the centre of the circle.

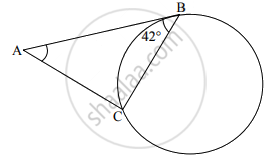
In the given figure, AB and AC are tangents to the circle. If ∠ABC = 42°, then the measure of ∠BAC is ______.
