Advertisements
Advertisements
Question
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle AOB

Solution
In the given fig, O is the centre of the circle and CA and CB are the tangents to the circle from C. Also, ∠ ACO = 30
P is any point on the circle. P and PB are joined.
To find : ∠AOB
Proof :
∴ ∠ ACB = 30° + 30° = 60°
∴∠ AOB + `∠`ACB = 180°
⇒ ∠ AOB + 60° = 180°
⇒ ∠ AOB = 180° - 60°
⇒ ∠ AOB = 120°
APPEARS IN
RELATED QUESTIONS
In Figure 1, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC
= 4 cm, then the length of AP (in cm) is
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
A chord of a length 16.8 cm is at a distance of 11.2 cm from the centre of a circle . Find the length of the chord of the same circle which is at a distance of 8.4 cm from the centre.
In fig., AB and DC are two chords of a circle with centre O. these chords when produced meet at P. if PB = Bern, BA = 7cm and PO = 14.5cm, find the radius of the circle.
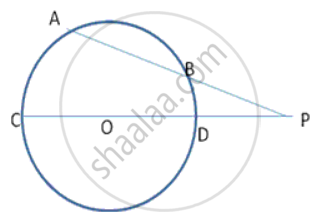
A point A is 17cm from the centre of the circle. The length of the tangent drawn from A to the circle is 15cm. find the radius of the circle.
If PA and PB are two tangents drawn from a point P to a circle with center C touching it A and B, prove that CP is the perpendicular bisector of AB.
In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

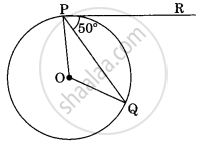
In figure, if O is the centre of a circle PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to ______.
The tangents drawn at the extremities of the diameter of a circle are ______.
In Question 5 above, if radii of the two circles are equal, prove that AB = CD.
