Advertisements
Advertisements
Question
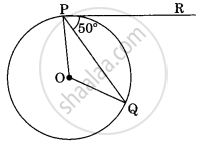
In figure, if O is the centre of a circle PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to ______.
Options
100°
80°
90°
75°
Solution
In figure, if O is the centre of a circle PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to 100°.
Explanation:
OP ⊥ PR ...[Tangent and radius are ⊥ to each other at the point of contact]
∠OPQ = 90° – 50° = 40°
OP = OQ ...[Radii]
∴ ∠OPQ = ∠OQP = 40°
In ∆OPQ,
⇒ ∠POQ + ∠OPQ + ∠OQP = 180°
⇒ ∠POQ + 40° + 40° = 180°
∠POQ = 180° – 80° = 100°.
RELATED QUESTIONS
In Figure 3, a right triangle ABC, circumscribes a circle of radius r. If AB and BC are of lengths of 8 cm and 6 cm respectively, find the value of r.

How many common tangents can be drawn to two circles, touching each
other externally?
In fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = 5 cm, find PT.
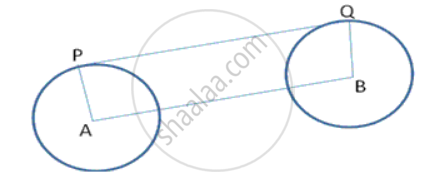
Calculate the length of direct common tangent to two circles of radii 3cm and Bern with their centres 13cm apart.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find AB.

Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
In the adjoining figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 30°, find the value of x.

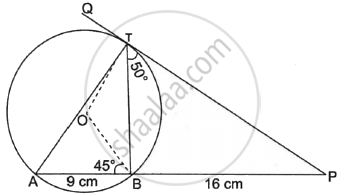
In the given figure, O is the centre of the circle. PQ is a tangent to the circle at T. Chord AB produced meets the tangent at P.
AB = 9 cm, BP = 16 cm, ∠PTB = 50° ∠OBA = 45°
Find:
- Length of PT
- ∠BAT
- ∠BOT
- ∠ABT
In the given diagram an isosceles ΔABC is inscribed in a circle with centre O. PQ is a tangent to the circle at C. OM is perpendicular to chord AC and ∠COM = 65°.

Find:
- ∠ABC
- ∠BAC
- ∠BCQ
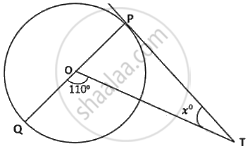
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is ______.