Advertisements
Advertisements
Question
In the given diagram an isosceles ΔABC is inscribed in a circle with centre O. PQ is a tangent to the circle at C. OM is perpendicular to chord AC and ∠COM = 65°.

Find:
- ∠ABC
- ∠BAC
- ∠BCQ
Solution
PQ is tangent to circle OM is perpendicular PQ chord AC and ∠COM = 65°
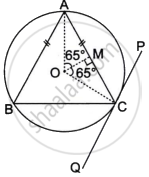
a. Here, ∠AOM = ∠COM = 65°
= 65° + 65°
= 130°
Now, ∠ABC =
=
= 65°
b. In ΔABC,
AB = AC
∠ABC = ∠ACB = 65° ...(Since, angles opposite to equal sides are equal)
∴ ∠BAC = 180° – (65° + 65°)
= 180° – 130°
= 50°
c. ∠OCQ = 90° ...(Since, angle between the radius and the tangent is 90°)
In ΔOMC,
∠OCM = 180° – (∠OMC + ∠MOC) ...[By angle sum property of triangle]
= 180° – (90° + 65°)
= 180° – 155°
= 25°
∠ACB = 65°
∠OCB = ∠ACB – ∠OCM
= 65° – 25°
= 40°
∠BCQ = ∠OCQ – ∠OCB
= 90° – 40°
= 50°
APPEARS IN
RELATED QUESTIONS
In the figure given below, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT = 60°, find ∠PRQ.

Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

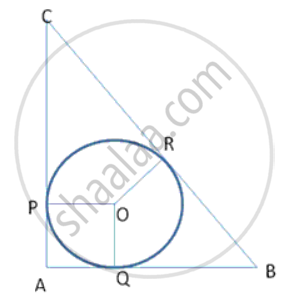
In following fig., ABC is a right- angled triangle at A with sides AB = 5 cm and BC = 13 cm . A circle with centre O has been inscribed in the triangle ABC. Calculate the radius of the incircle.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find the length of tangent PT.

In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate ∠ PAD.

ABC is a right triangle with angle B = 90º. A circle with BC as diameter meets by hypotenuse AC at point D. Prove that: BD2 = AD × DC.
Construct a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
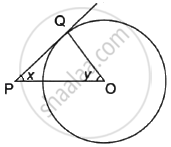
In the given figure, PQ is a tangent to the circle with centre O. If ∠OPQ = x, ∠POQ = y, then x + y is ______.
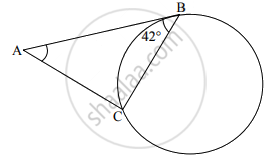
In the given figure, AB and AC are tangents to the circle. If ∠ABC = 42°, then the measure of ∠BAC is ______.
