Advertisements
Advertisements
Question
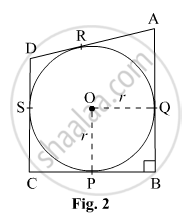
In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

Solution
In the given figure, we have an external point X from where two tangents, XP and XQ, are drawn to the circle.
XP = XQ (The lengths of the tangents drawn from an external point to the circle are equal.)
Similarly, we have:
AP = AR
BQ = BR
Now, XP = XA + AP ...(1)
XQ = XB + BQ ...(2)
On putting AP = AR in equation (1) and BQ = BR in equation (2), we get:
XP = XA + AR
XQ = XB + BR
Since XP and XQ are equal, we have:
XA + AR = XB + BR
Hence, proved.
APPEARS IN
RELATED QUESTIONS
In Fig. 7, two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of `(DO')/(CO')`

If the angle between two tangents drawn from an external point P to a circle of radius a and centre O, is 60°, then find the length of OP
In triangle PQR, PQ = 24 cm, QR = –7 cm and ∠PQR = 90°. Find the radius of the inscribed circle.

In Fig.2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5 cm, then the radius of the circle (in cm.) is:
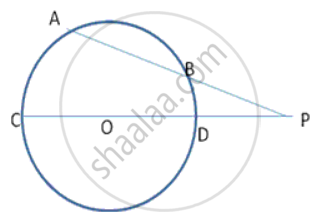
In fig., AB and DC are two chords of a circle with centre O. these chords when produced meet at P. if PB = Bern, BA = 7cm and PO = 14.5cm, find the radius of the circle.
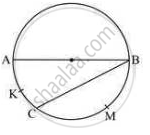
In the following figure, seg AB is a diameter of the circle, m (arc AKC) = 40°. Find the value of m (arc BMC).
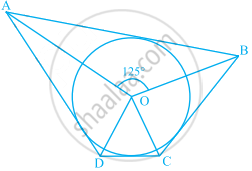
In figure, if ∠AOB = 125°, then ∠COD is equal to ______.
Find the value of ∠DCE.

ABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ = 65°, then ∠BCD is ______

In the adjoining figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 30°, find the value of x.

