Advertisements
Advertisements
Question
If the angle between two tangents drawn from an external point P to a circle of radius a and centre O, is 60°, then find the length of OP
Solution
Let PA and PB be the two tangents drawn to the circle with centre O and radius a such that ∠APB=60°
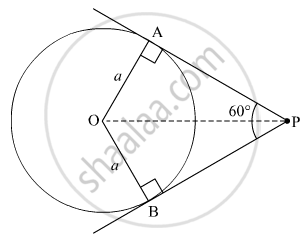
In ∆OPB and ∆OPA
OB = OA = a (Radii of the circle)
∠OBP = ∠OAP=90° (Tangents are perpendicular to radius at the point of contact)
BP = PA (Lengths of tangents drawn from an external point to the circle are equal)
So, ∆OPB ≌ ∆OPA (SAS Congruence Axiom)
∴ ∠OPB = ∠OPA=30° (CPCT)
Now,
In ∆OPB
Thus the length of OP is 2a
APPEARS IN
RELATED QUESTIONS
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

In triangle PQR, PQ = 24 cm, QR = –7 cm and ∠PQR = 90°. Find the radius of the inscribed circle.

Draw Δ ABC such that, AB = 8 cm, BC = 6 cm and ∠ B = 90°. Draw seg BD
perpendicular to hypotenuse AC. Draw a circle passing through points
B, D, A. Show that line CB is a tangent of the circle.
A chord of a length 16.8 cm is at a distance of 11.2 cm from the centre of a circle . Find the length of the chord of the same circle which is at a distance of 8.4 cm from the centre.
In followinf fig., two concentric circles with centre 0 are of radii 5 cm and 3 cm. from an external point P, tangents PA and PB are drawn to these circles. If AP = 12cm, find BP.
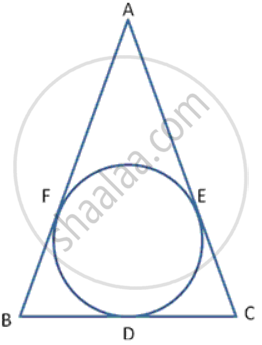
In following figure , the incircle of Δ ABC , touches the sides BC , CA and AB at D , E and F respectively. Show AF + BD + CE = AE + BF + CD
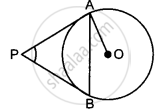
In the figure PA and PB are tangents to the circle with centre O. If ∠APB = 60°, then ∠OAB is ______
In the figure, PQ and PR are tangents to a circle with centre A. If ∠QPA=27°, then ∠QAR equals to ______
In figure, O is the centre of a circle of radius 5 cm, T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.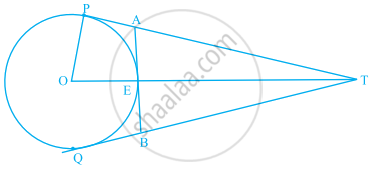
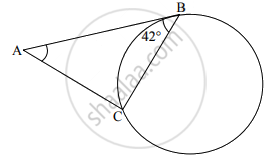
In the given figure, AB and AC are tangents to the circle. If ∠ABC = 42°, then the measure of ∠BAC is ______.
