Advertisements
Advertisements
Question
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

Solution
In cyclic quadrilateral ABCD,
∠B + ∠D = 180° (opp angles of the cyclic quad are supplementary)
⇒ 100° + ∠ADC = 180°
=> ∠ADC = 80°
Now in ΔACD
∠ACD + ∠CAD + ∠ADC = 180°
40° + ∠CAD + 80° = 180°
∠CAD = 180° - 120° = 60°
Now ∠DCT = ∠CAD (angles in the alternate segment)
∴ ∠DCT = 60°
APPEARS IN
RELATED QUESTIONS
How many tangents can a circle have?
A tangent to a circle intersects it in ______ point (s).
In the given figure O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of a circle.

In the given figure, find TP if AT = 16 cm and AB = 12 cm.

In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

If Δ ABC is isosceles with AB = AC and C (O, r) is the incircle of the ΔABC touching BC at L,prove that L bisects BC.
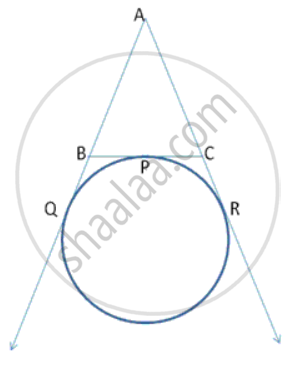
In following fig., a circle is touching the side BC of Δ ABC at P and AB and AC produced at Q and R respectively. Prove that AQ is half the perimeter of Δ ABC.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate ∠ PAD.

Tangents from an external point to a circle are ______
Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
