Advertisements
Advertisements
Question
If Δ ABC is isosceles with AB = AC and C (O, r) is the incircle of the ΔABC touching BC at L,prove that L bisects BC.
Solution
Let us first put the given data in the form of a diagram.
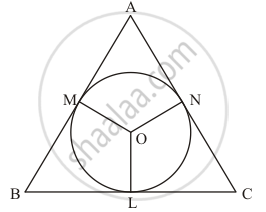
It is given that triangle ABC is isosceles with
AB = AC …… (1)
By looking at the figure we can rewrite the above equation as,
AM + MB = AN + NC
From the property of tangents we know that the length of two tangents drawn to a circle from the same external point will be equal. Therefore,
AM = AN
Let us substitute AN with AM in the equation (1). We get,
AM + MB = AM + NC
MB = NC …… (2)
From the property of tangents we know that the length of two tangents drawn from the same external point will be equal. Therefore we have,
MB = BL
NC = LC
But from equation (2), we have found that
MB = NC
Therefore,
BL = LC
Thus we have proved that point L bisects side BC.
APPEARS IN
RELATED QUESTIONS
Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
In fig. 5 is a chord AB of a circle, with centre O and radius 10 cm, that subtends a right angle at the centre of the circle. Find the area of the minor segment AQBP. Hence find the area of major segment ALBQA. (use π = 3.14)

In Figure 3, a right triangle ABC, circumscribes a circle of radius r. If AB and BC are of lengths of 8 cm and 6 cm respectively, find the value of r.

A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle AOB

In the following figure, seg AB is a diameter of the circle, m (arc AKC) = 40°. Find the value of m (arc BMC).
In Fig. the incircle of ΔABC touches the sides BC, CA, and AB at D, E respectively. Show that: AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)

Find the value of ∠DCE.

Assertion (A): A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R): The lengths of tangents drawn from an external point to a circle are equal.
If O is centre of a circle and Chord PQ makes an angle 50° with the tangent PR at the point of contact P, then the angle subtended by the chord at the centre is ______.