Advertisements
Advertisements
प्रश्न
If Δ ABC is isosceles with AB = AC and C (O, r) is the incircle of the ΔABC touching BC at L,prove that L bisects BC.
उत्तर
Let us first put the given data in the form of a diagram.
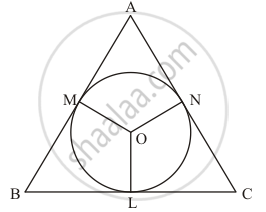
It is given that triangle ABC is isosceles with
AB = AC …… (1)
By looking at the figure we can rewrite the above equation as,
AM + MB = AN + NC
From the property of tangents we know that the length of two tangents drawn to a circle from the same external point will be equal. Therefore,
AM = AN
Let us substitute AN with AM in the equation (1). We get,
AM + MB = AM + NC
MB = NC …… (2)
From the property of tangents we know that the length of two tangents drawn from the same external point will be equal. Therefore we have,
MB = BL
NC = LC
But from equation (2), we have found that
MB = NC
Therefore,
BL = LC
Thus we have proved that point L bisects side BC.
APPEARS IN
संबंधित प्रश्न
In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

A chord of a length 16.8 cm is at a distance of 11.2 cm from the centre of a circle . Find the length of the chord of the same circle which is at a distance of 8.4 cm from the centre.
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
Calculate the length of direct common tangent to two circles of radii 3cm and Bern with their centres 13cm apart.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate : ∠CDB

Find the value of ∠DCE.

In Question 5 above, if radii of the two circles are equal, prove that AB = CD.
A tangent JK is drawn to a circle with centre C such that CK = 6 cm and ∠CKJ = 60°. Find the length of the tangent JK.

A circle of radius 5.2 cm has two tangents AB and CD parallel to each other. What is the distance between the two tangents?
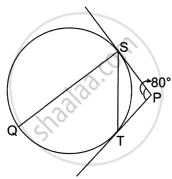
In the given diagram, PS and PT are the tangents to the circle. SQ || PT and ∠SPT = 80°. The value of ∠QST is ______.