Advertisements
Advertisements
प्रश्न
Two tangent segments PA and PB are drawn to a circle with center O such that ∠APB =120°. Prove that OP = 2AP
उत्तर
A + P
OP bisects ∠APB
∠APO = ∠OPB =`1/2`∠𝐴𝑃𝐵 =`1/2`× 120° = 60°
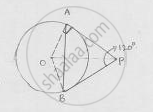
At point A
OA ⊥ AP, ∠OAP = 90°
In ΔPDA, cos 60° =`(AP)/(DP)`
`1/2=(AP)/(DP)`⇒ 𝐷𝑃 = 2𝐴𝑃
APPEARS IN
संबंधित प्रश्न
Fill in the blanks:
Segment of a circle is the region between an arc and __________ of the circle.
Write True or False. Give reasons for your answers.
If a circle is divided into three equal arcs, each is a major arc.
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
O is the centre of a circle of radius 10 cm. P is any point in the circle such that OP = 6 cm. A is the point travelling along the circumference. x is the distance from A to P. what are the least and the greatest values of x in cm? what is the position of the points O, P and A at these values?
If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, then the diameter of the larger circle (in cm) is:
In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

In the given figure, a ∆ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC are of lengths 8 cm and 6 cm respectively. Find the lengths of sides AB and AC, when area of ∆ABC is 84 cm2.

In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.

Find the diameter of the circle
Radius = 8 cm
From the figure, identify the centre of the circle.