Advertisements
Advertisements
प्रश्न
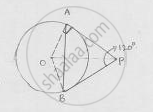
Two tangent segments PA and PB are drawn to a circle with center O such that ∠APB =120°. Prove that OP = 2AP
उत्तर
A + P
OP bisects ∠APB
∠APO = ∠OPB =`1/2`∠𝐴𝑃𝐵 =`1/2`× 120° = 60°
At point A
OA ⊥ AP, ∠OAP = 90°
In ΔPDA, cos 60° =`(AP)/(DP)`
`1/2=(AP)/(DP)`⇒ 𝐷𝑃 = 2𝐴𝑃
APPEARS IN
संबंधित प्रश्न
In the given figure, the incircle of ∆ABC touches the sides BC, CA and AB at D, E, F respectively. Prove that AF + BD + CE = AE + CD + BF = `\frac { 1 }{ 2 } ("perimeter of ∆ABC")`
O is the center of a circle of radius 8cm. The tangent at a point A on the circle cuts a line through O at B such that AB = 15 cm. Find OB
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO~Δ ABC.

ture or false v
The degree measure of a semi-circle is 180°.
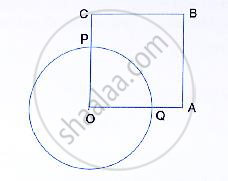
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC
at P and OA at Q. Prove that:
(i) ΔOPA ≅ ΔOQC, (ii) ΔBPC ≅ ΔBQA.
Find the length of the chord of a circle in the following when:
Radius is 6.5 cm and the distance from the centre is 2.5 cm
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA
Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre
In the given figure, O is the centre of the circle. Shade the smaller segment of the circle formed by CP.