Advertisements
Advertisements
प्रश्न
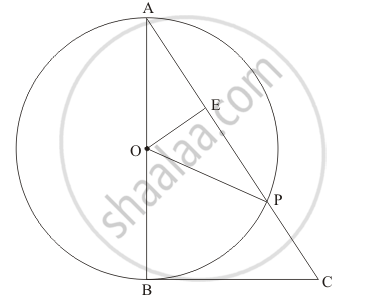
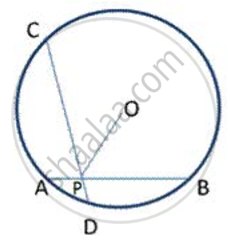
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO~Δ ABC.

उत्तर
The figure given in the question is below

Let us first take up ΔAOP.
We have,
OA = OP (Since they are the radii of the same circle)
Therefore, ΔAOP is an isosceles triangle. From the property of isosceles triangle,
we know that, when a median drawn to the unequal side of the triangle will be
perpendicular to the unequal side. Therefore,
∠OEA=90°
Now let us take up ΔAOE and ΔABC.
We know that the radius of the circle will always be perpendicular to the tangent at
the point of contact. In this problem, OB is the radius and BC is the tangent
and B is the point of contact. Therefore,
∠ABC=90°
Also, from the property of isosceles triangle we have found that
∠OEA=90°
Therefore,
∠ABC=∠OEA
∠A is the common angle to both the triangles.
Therefore, from AA postulate of similar triangles,
ΔAOE~ΔABC
Thus we have proved
संबंधित प्रश्न
Fill in the blanks:
The centre of a circle lies in ____________ of the circle.
Fill in the blanks:
A point, whose distance from the centre of a circle is greater than its radius lies in __________ of the circle. (exterior/ interior)
From an external point P, tangents PA and PB are drawn to the circle with centre O. If CD is the tangent to the circle at point E and PA = 14 cm. Find the perimeter of ABCD.
In the fig. a circle is inscribed in a quadrilateral ABCD in which ∠B = 90° if AD = 23cm,
AB = 29cm and DS = 5cm, find the radius of the circle.
O is the centre of a circle of radius 10 cm. P is any point in the circle such that OP = 6 cm. A is the point travelling along the circumference. x is the distance from A to P. what are the least and the greatest values of x in cm? what is the position of the points O, P and A at these values?
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

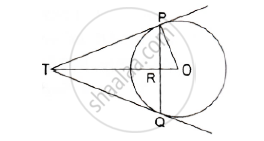
PQ is a chord of length 4.8 cm of a circle of radius 3cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.
In two concentric circles, a chord of length 8 cm of the large circle touches the smaller circle. If the radius of the larger circle is 5 cm, then find the radius of the smaller circle.
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the lengths of TP and TQ.

In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
An equilateral triangle ABC is inscribed in a circle with centre O. The measures of ∠BOCis
In the given figure, if ∠ABC = 45°, then ∠AOC =
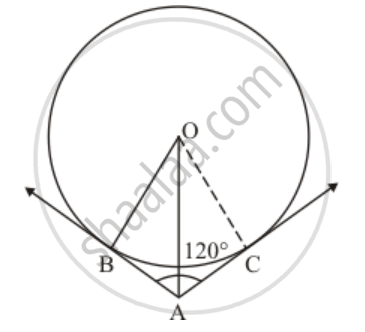
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO ∼ Δ ABC.
AB and CD are two equal chords of a drde intersecting at Pas shown in fig. P is joined to O , the centre of the cirde. Prove that OP bisects ∠ CPB.
ABC is a right triangle in which ∠B = 90°. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
In the given figure, the area enclosed between the two concentric circles is 770 cm2. If the radius of the outer circle is 21 cm, calculate the radius of the inner circle.
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

Use the figure given below to fill in the blank:
Tangent to a circle is _______.

The ratio between the circumference and diameter of any circle is _______
A part of circumference of a circle is called as _______
A line through the point of contact and passing through centre of the circle is known as ______
The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is ______
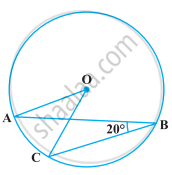
In the following figure, if ∠ABC = 20º, then ∠AOC is equal to ______.
If AOB is a diameter of a circle and C is a point on the circle, then AC2 + BC2 = AB2.
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
From the figure, identify three radii.
A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
What is the area of a semi-circle of diameter ‘d’?
