Advertisements
Advertisements
प्रश्न
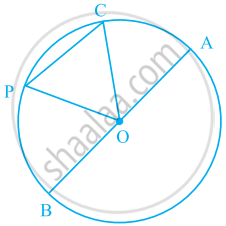
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

उत्तर
Given, PA and PB are the tangents to a circle with center O and CD is a tangent at E and PA = 14 cm.
Tangents drawn from an external point are equal.
∴ PA = PB, CA = CE and DB = DE
Perimeter of Δ PCD = PC + CD + PD
= (PA- CA)+( CE +DE) +( PB- DB)
= (PA -CE)+ (CE+ DE)+( PB- DE)
=(PA+ PB)
= 2PA(∵ PA= PB)
=(2×14) cm
= 28 cm
=28 cm
∴ Perimeter of ΔPCD = 28cm.
APPEARS IN
संबंधित प्रश्न
ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
If from any point on the common chord of two intersecting circles, tangents be drawn to circles, prove that they are equal.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
On a semi-circle with AB as diameter, a point C is taken, so that m (∠CAB) = 30°. Find m(∠ACB) and m (∠ABC).
Use the figure given below to fill in the blank:
________ is a radius of the circle.
Construct a triangle ABC with AB = 5 cm, ∠B = 60° and BC = 6. 4 cm. Draw the incircle of the triangle ABC.
Construct a triangle XYZ in which XY = YZ= 4.5 cm and ZX = 5.4 cm. Draw the circumcircle of the triangle and measure its circumradius.
The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre
If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see figure), prove that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.
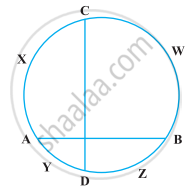
In the given figure, O is the centre of the circle. Name all chords of the circle.