Advertisements
Advertisements
प्रश्न
If from any point on the common chord of two intersecting circles, tangents be drawn to circles, prove that they are equal.
उत्तर
Let the two circles intersect at points X and Y.
XY is the common chord.
Suppose ‘A’ is a point on the common chord and AM and AN be the tangents drawn A to the circle
We need to show that AM = AN.
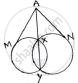
In order to prove the above relation, following property will be used.
“Let PT be a tangent to the circle from an external point P and a secant to the circle through
P intersects the circle at points A and B, then 𝑃𝑇2 = 𝑃𝐴 × 𝑃𝐵"
Now AM is the tangent and AXY is a secant ∴ 𝐴𝑀2 = 𝐴𝑋 × 𝐴𝑌 … . . (𝑖)
AN is a tangent and AXY is a secant ∴ 𝐴𝑁2 = 𝐴𝑋 × 𝐴𝑌 … . . (𝑖𝑖)
From (i) & (ii), we have 𝐴𝑀2 = 𝐴𝑁2
∴ AM = AN
APPEARS IN
संबंधित प्रश्न
In the given figure, PQ is a chord of length 8cm of a circle of radius 5cm. The tangents at P and Q intersect at a point T. Find the length TP

Fill in the blank:
A point whose distance from the centre of a circle is greater than its radius lies in ..................... of the circle.
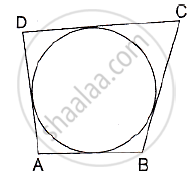
In the adjoining figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB=6cm, BC=9cm and CD=8 cm. Find the length of side AD.
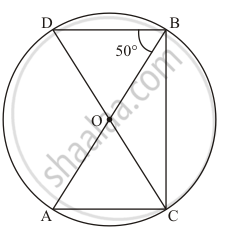
In the given figure, AB and CD are diameters of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
One chord of a circle is known to be 10 cm. The radius of this circle must be
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then

Draw a line AB = 8.4 cm. Now draw a circle with AB as diameter. Mark a point C on the circumference of the circle. Measure angle ACB.
State, if the following statement is true or false:
Every diameter bisects a circle and each part of the circle so obtained is a semi-circle.
The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle
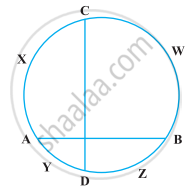
If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see figure), prove that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.