Advertisements
Advertisements
प्रश्न
The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle
उत्तर
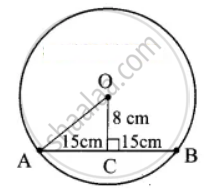
Distance AC = `1/2 xx "Length of chord"`
= `1/2 xx 30`
= 15 cm
Distance from the centre = 8 cm
In ΔOAC Radius (OA) = `sqrt("AC"^2 + "OC"^2)`
= `sqrt(15^2 + 8^2)`
= `sqrt(225 + 64)`
= `sqrt(289)`
= 17
Radius of the circle = 17 cm.
APPEARS IN
संबंधित प्रश्न
PA and PB are tangents from P to the circle with centre O. At point M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

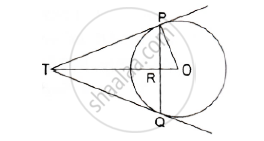
PQ is a chord of length 4.8 cm of a circle of radius 3cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.
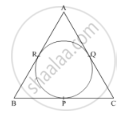
In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
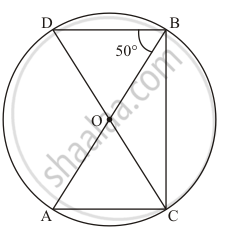
In the given figure, AB and CD are diameters of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is
Can the length of a chord of a circle be greater than its diameter ? Explain.
In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

