Advertisements
Advertisements
प्रश्न
The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle
उत्तर
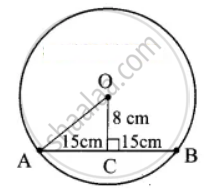
Distance AC = `1/2 xx "Length of chord"`
= `1/2 xx 30`
= 15 cm
Distance from the centre = 8 cm
In ΔOAC Radius (OA) = `sqrt("AC"^2 + "OC"^2)`
= `sqrt(15^2 + 8^2)`
= `sqrt(225 + 64)`
= `sqrt(289)`
= 17
Radius of the circle = 17 cm.
APPEARS IN
संबंधित प्रश्न
Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
Fill in the blanks:
Segment of a circle is the region between an arc and __________ of the circle.
In figure PA and PB are tangents from an external point P to the circle with centre O. LN touches the circle at M. Prove that PL + LM = PN + MN
A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].
Draw circle with diameter: 8.4 cm
In above case, measure the length of the radius of the circle drawn.
C(O, r1) and C(O, r2) are two concentric circles with r1 > r2 AB is a chord of C(O, r1) touching C(O, r2) at C then ______
If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is ______
Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s – b.
