Advertisements
Advertisements
प्रश्न
In figure PA and PB are tangents from an external point P to the circle with centre O. LN touches the circle at M. Prove that PL + LM = PN + MN
उत्तर

Given
O is Centre of circle
PA and PB are tangents
We know that
The tangents drawn from external point to the circle are equal in length.
From point P, PA = PB
⇒ PL + AL = PN + NB …. (i)
From point L & N, AL = LM and MN = NB } …. Substitute in (i)
PL + Lm = PN + MN
⇒ Hence proved.
APPEARS IN
संबंधित प्रश्न
Write True or False. Give reasons for your answers.
A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BC and DC into which BC is divided by the point of contact D, are of
lengths 6cm and 9cm respectively. If the area of 2 ΔABC = 54cm2 then find the lengths of sides AB and AC.

In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.

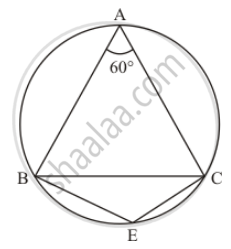
In the given figure, ΔABC is an equilateral triangle. Find m∠BEC.
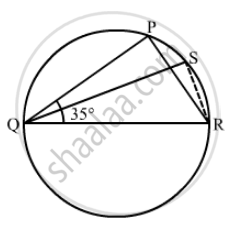
In the given figure, ΔPQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.
Find the area of a circle of radius 7 cm.
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is ______
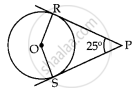
In the given figure, if ZRPS = 25°, the value of ZROS is ______
If an isosceles triangle ABC, in which AB = AC = 6 cm, is inscribed in a circle of radius 9 cm, find the area of the triangle.
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
