Advertisements
Advertisements
प्रश्न
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
उत्तर
Given: O is the circumcenter of the triangle ABC and D is the midpoint of BC.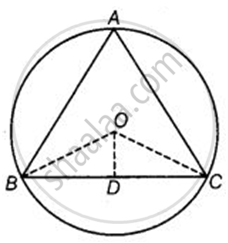
To prove: ∠BOD = ∠A
Join OB and OC.
In ΔOBD and ΔCD,
OD = OD ...(Common side)
DB = Dc ...(D is the midpoint of BC)
OB = OC ...(Both are radius of the circle)
By SSS congruence rule, ΔOBD ≅ ΔOCD.
∴ ∠BOD = ∠COD = x (say) ...(By CPCT)
Since, angle subtended by an arc at the center of the circle is twice the angle subtended by it at any other point in the remaining part of the circle, we have:
2∠BAC = ∠BOC
⇒ 2∠BAC = ∠BOD + ∠DOC
⇒ 2∠BAC = x + x
⇒ 2∠BAC = 2x
⇒ ∠BAC = x
⇒ ∠BAC = ∠BOD
Hence proved.
APPEARS IN
संबंधित प्रश्न
In the given figure, PQ and RS are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersects PQ at A and RS at B. Prove that ∠AOB = 90º
Two circles touch internally. The sum of their areas is 116 π cm2 and the distance between their centres is 6 cm. Find the radii of the circles ?
If the difference between the circumference and the radius of a circle is 37 cm, then using`22/7`, the circumference (in cm) of the circle is:
A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

The greatest chord of a circle is called its
In the given figure, if ∠ABC = 45°, then ∠AOC =
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s – b.
In the following figure, if ∠DAB = 60º, ∠ABD = 50º, then ∠ACB is equal to ______.