Advertisements
Advertisements
प्रश्न
On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides. Prove that ∠BAC = ∠BDC.
उत्तर
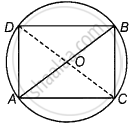
Given: ΔACB and ΔADB are two right angled triangles with common hypotenuse AB.
To prove: ∠BAC = ∠BDC
Construction: Join CD.
Proof: Let O be the mid-point of AB
Then, OA = OB = OC = OD.
Since, mid-point of the hypotenuse of a right triangle is equidistant from its verticles.
Now, draw a circle to pass through the points A, B, C and D with O as centre and radius equal to OA.
We know that, angles in the same segment of a circle are equal.
From the figure, ∠BAC and ∠BDC are angles of same segment BC.
∴ ∠BAC = ∠BDC
Hence proved.
APPEARS IN
संबंधित प्रश्न
If the tangent at point P to the circle with center O cuts a line through O at Q such that PQ= 24cm and OQ = 25 cm. Find the radius of circle
In the following figure, AB is the diameter of a circle with centre O and CD is the chord with length equal to radius OA.
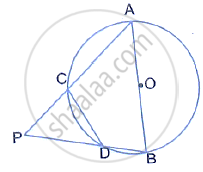
Is AC produced and BD produced meet at point P; show that ∠APB = 60°
In the given figure, O is the centre of the circle. Find ∠CBD.

In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.

In Fig. 8.79, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find ∠1 + ∠2.

The circle which passes through all the vertices of a triangle is called ______.
In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
In the given figure, O is the centre of the circle. Name all radii of the circle.