Advertisements
Advertisements
Question
On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides. Prove that ∠BAC = ∠BDC.
Solution
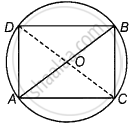
Given: ΔACB and ΔADB are two right angled triangles with common hypotenuse AB.
To prove: ∠BAC = ∠BDC
Construction: Join CD.
Proof: Let O be the mid-point of AB
Then, OA = OB = OC = OD.
Since, mid-point of the hypotenuse of a right triangle is equidistant from its verticles.
Now, draw a circle to pass through the points A, B, C and D with O as centre and radius equal to OA.
We know that, angles in the same segment of a circle are equal.
From the figure, ∠BAC and ∠BDC are angles of same segment BC.
∴ ∠BAC = ∠BDC
Hence proved.
APPEARS IN
RELATED QUESTIONS
In fig., O is the centre of the circle, PA and PB are tangent segments. Show that the quadrilateral AOBP is cyclic.
In fig.. O is the center of the circle and BCD is tangent to it at C. Prove that ∠BAC +
∠ACD = 90°
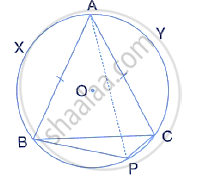
In the given figure ABC is an isosceles triangle and O is the centre of its circumcircle. Prove that AP bisects angle BPC .
Two circles touch internally. The sum of their areas is 116 π cm2 and the distance between their centres is 6 cm. Find the radii of the circles ?
In the given figure, the area enclosed between the two concentric circles is 770 cm2. If the radius of the outer circle is 21 cm, calculate the radius of the inner circle.
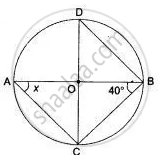
If O is the centre of the circle, find the value of x in each of the following figures
Use the figure given below to fill in the blank:
Diameter = 2 x ________

Draw circle with diameter: 6 cm
In above case, measure the length of the radius of the circle drawn.
The length of tangent from an external point on a circle is always greater than the radius of the circle.
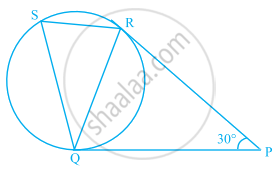
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
[Hint: Draw a line through Q and perpendicular to QP.]