Advertisements
Advertisements
Question
Two chords AB and AC of a circle subtends angles equal to 90º and 150º, respectively at the centre. Find ∠BAC, if AB and AC lie on the opposite sides of the centre.
Solution
In triangle BOA,
OB = OA ...[Both are the radius of circle]
∠OAB = ∠OBA ...(i) [Angle opposite to equal sides are equal]
Now, In triangle OAB,
∠OBA + ∠AOB + ∠AOC = 180° ...[By angle sum property of a triangle]
∠OAB + ∠OAB + 90° = 180° ...[From equation (i)]
2∠OAB = 180° – 90°
2∠OAB = 90°
∠OAB = 45°
Again, in triangle AOC,
AO = OC ...[Radii or circle]
∠OCA = ∠OAC ...(ii) [Angle opposite to equal sides are equal]
Now, by angle sum property of a triangle,
∠AOC + ∠OAC + ∠OCA = 180°
150° + 2∠OAC = 180° ...[From equation (ii)]
2∠OAC = 180° – 150°
2∠OAC = 30°
∠OAC = 15°
∠BAC = ∠OAB + ∠OAC = 45° + 15° = 60°
APPEARS IN
RELATED QUESTIONS
If PA and PB are tangents from an outside point P. such that PA = 10 cm and ∠APB = 60°. Find the length of chord AB.
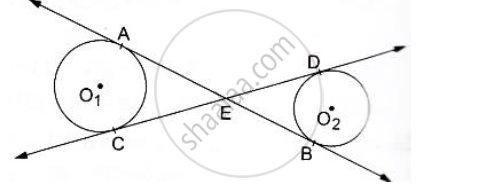
In the given figure common tangents AB and CD to the two circles with centres O1 and O2 intersect at E. Prove that AB=CD
In a cyclic quadrilateral ABCD if AB || CD and ∠B = 70°, find the remaining angles.
AB is a chord of a circle with centre O , AOC is a diameter and AT is the tangent at A as shown in Fig . 10.70. Prove that \[\angle\]BAT = \[\angle\] ACB.
In the given figure, a ∆ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC are of lengths 8 cm and 6 cm respectively. Find the lengths of sides AB and AC, when area of ∆ABC is 84 cm2.


In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
Draw a circle of radius 6 cm. In the circle, draw a chord AB = 6 cm.
(i) If O is the center of the circle, join OA and OB.
(ii) Assign a special name to ∆AOB
(iii) Write the measure of angle AOB.
In the adjoining figure, seg DE is the chord of the circle with center C. seg CF⊥ seg DE and DE = 16 cm, then find the length of DF?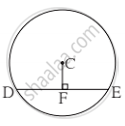
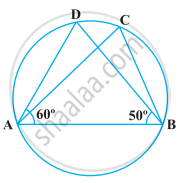
In the following figure, if ∠DAB = 60º, ∠ABD = 50º, then ∠ACB is equal to ______.
In the following figure, if AOB is a diameter and ∠ADC = 120°, then ∠CAB = 30°.