Advertisements
Advertisements
Question
In the given figure, a ∆ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC are of lengths 8 cm and 6 cm respectively. Find the lengths of sides AB and AC, when area of ∆ABC is 84 cm2.

Solution

Here, D, E and F are the points of contact of the circle with the sides BC, AB and AC, respectively.
OD = OE = OF = 4 cm (Radii of the circle)
We know that the lengths of tangents drawn from an external point to a circle are equal.
∴ BD = BE = 8 cm
CD = CF = 6 cm
AE = AF = x cm (say)
So, BC = BD + CD = 8 cm + 6 cm = 14 cm
AB = AE + BE = x cm + 8 cm = (x + 8) cm
AC = AF + FC = x cm + 6 cm = (x + 6) cm
Also, the tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ OD ⊥ BC, OE ⊥ AB and OF ⊥ AC
Now,
ar(∆OBC) + ar(∆OAB) + ar(∆OCA) = ar(∆ABC)
\[\therefore \frac{1}{2} \times BC \times OD + \frac{1}{2} \times AB \times OE + \frac{1}{2} \times AC \times OF = 84 {cm}^2 \]
\[ \Rightarrow \frac{1}{2} \times 14 \times 4 + \frac{1}{2} \times \left( x + 8 \right) \times 4 + \frac{1}{2} \times \left( x + 6 \right) \times 4 = 84\]
\[ \Rightarrow 28 + 2x + 16 + 2x + 12 = 84\]
\[ \Rightarrow 4x + 56 = 84\]
\[\Rightarrow 4x = 84 - 56 = 28\]
\[ \Rightarrow x = 7\]
∴ AB = (x + 8) cm = (7 + 8) cm = 15 cm
AC = (x + 6) cm = (7 + 6) cm = 13 cm
Hence, the lengths of sides AB and AC are 15 cm and 13 cm, respectively.
RELATED QUESTIONS
Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
ABCD is a quadrilateral such that ∠D = 90°. A circle (O, r) touches the sides AB, BC, CD and DA at P,Q,R and If BC = 38 cm, CD = 25 cm and BP = 27 cm, find r.
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
From a point P, two tangents PA and PB are drawn to a circle with center O. If OP =
diameter of the circle shows that ΔAPB is equilateral.
true or false
A circle is a plane figure.
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

In fig. 3 are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP ?

In Fig. 1, the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is ?
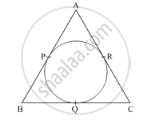
Tangents PA and PB are drawn from an external point P to two concentric circles with centre O and radii 8 cm and 5 cm respectively, as shown in Fig. 3. If AP = 15 cm, then find the length of BP.
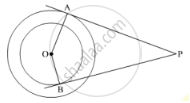
In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
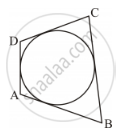
In Figure 3, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of the side AD.
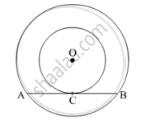
If the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is
An equilateral triangle ABC is inscribed in a circle with centre O. The measures of ∠BOCis
In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.

In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.

Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.

In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA
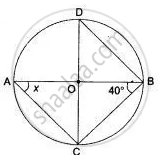
If O is the centre of the circle, find the value of x in each of the following figures
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

Draw a circle of diameter 7 cm. Draw two radii of this circle such that the angle between these radii is 90°. Shade the minor sector obtained. Write a special name for this sector.
State, if the following statement is true or false:
Every diameter bisects a circle and each part of the circle so obtained is a semi-circle.
The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre
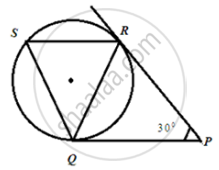
In the following figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, then ∠RQS.
If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
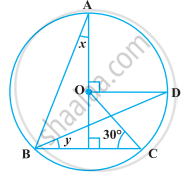
In the following figure, O is the centre of the circle, ∠BCO = 30°. Find x and y.
From the figure, identify a sector.

From the figure, identify a segment.

