Advertisements
Advertisements
Question
Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
Solution
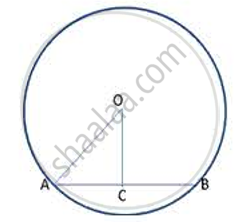
AC = CB ----(1) (Perpendicular from centre to a chord bisects the chord)
In right t. ACO,
By Pythagoras theorem, OA2 = OC2 + AC2
132 -122 = AC2
AC2 = 169 - 144 = 25
AC = 5 cm
∴ length of chord AB = 2AC (from (1))
APPEARS IN
RELATED QUESTIONS
In Fig. 8, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle.

Prove that in two concentric circles, the chord of the larger circle which touches the smaller circle, is bisected at the point of contact.
If AB, AC, PQ are tangents in Fig. and AB = 5cm find the perimeter of ΔAPQ.
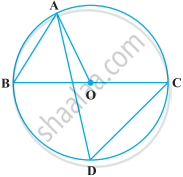
In the given figure ABC is an isosceles triangle and O is the centre of its circumcircle. Prove that AP bisects angle BPC .
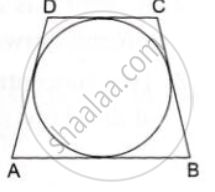
In the given figure, a circle touches all the four sides of a quadrilateral ABCD whose three sides are AB = 6cm, BC=7cm and CD=4 cm. Find AD.
In the given figure, O is the centre of the two concentric circles of radii 4 cm and 6cm respectively. AP and PB are tangents to the outer and inner circle respectively. If PA = 10cm, find the length of PB up to one place of the decimal.
In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29cm, AD = 23cm, ∠B = 90° and DS=5cm then find the radius of the circle.

In the given figure, O is the centre of the circle. If ∠BOD = 160°, find the values of x and y.

The circle which passes through all the vertices of a triangle is called ______.
In the following figure, BC is a diameter of the circle and ∠BAO = 60º. Then ∠ADC is equal to ______.