Advertisements
Advertisements
Question
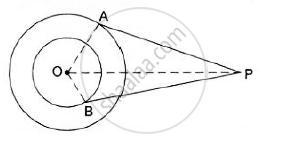
In the given figure, O is the centre of the two concentric circles of radii 4 cm and 6cm respectively. AP and PB are tangents to the outer and inner circle respectively. If PA = 10cm, find the length of PB up to one place of the decimal.
Solution
Given, O is the center of two concentric circles of radii OA = 6 cm and OB = 4 cm.
PA and PB are the two tangents to the outer and inner circles respectively and PA = 10 cm.
Now, tangent drawn from an external point is perpendicular to the radius at the point of contact.
∴∠OAP = ∠OBP = 90°
∴ From right – angled ΔOAP,OP2 = OA2 + PA2
`⇒OP = sqrt(OA^2 + PA^2)`
`⇒ OP = sqrt (6^2 +10^2)`
`⇒ OP = sqrt( 136cm)`.
∴ From right – angled `Δ OAP,OP^2 = OB^2 + PB^2`
`⇒ PB = sqrt(OP^2 -OB^2)`
`⇒ PB = sqrt(136-16)`
`⇒ PB= sqrt(120cm)`
⇒ PB = 109.cm.
∴ The length of PB is 10.9 cm.
APPEARS IN
RELATED QUESTIONS
From an external point P, tangents PA and PB are drawn to the circle with centre O. If CD is the tangent to the circle at point E and PA = 14 cm. Find the perimeter of ABCD.
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:
- ∠AOB,
- ∠ACB,
- ∠ABC.
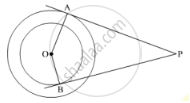
Tangents PA and PB are drawn from an external point P to two concentric circles with centre O and radii 8 cm and 5 cm respectively, as shown in Fig. 3. If AP = 15 cm, then find the length of BP.
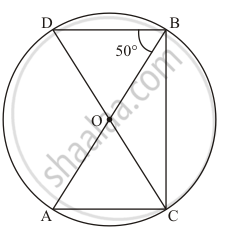
In the given figure, AB and CD are diameters of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

Draw a line AB = 8.4 cm. Now draw a circle with AB as diameter. Mark a point C on the circumference of the circle. Measure angle ACB.
Construct a triangle PQR in which, PQ = QR = RP = 5.7 cm. Draw the incircle of the triangle and measure its radius.
Find the radius of the circle
Diameter = 30 cm
If the angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre ‘O’ is 90°, then OP = ______
AB is a chord of a circle with centre O. AOC is diameter of circle, AT is a tangent at A.
Write answers of the following questions:
- Draw the figure using the given information.
- Find the measures of ∠CAT and ∠ABC with reasons.
- Whether ∠CAT and ∠ABC are congruent? Justify your answer.
