Advertisements
Advertisements
Question
Construct a triangle PQR in which, PQ = QR = RP = 5.7 cm. Draw the incircle of the triangle and measure its radius.
Solution
Steps of Construction:
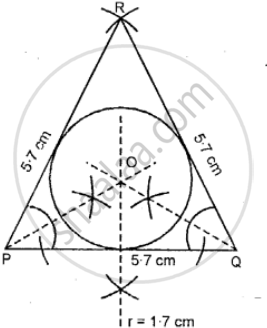
(i) Draw an equilateral ∆ RPQ in which PQ = QR = RP = 5.7 cm each.
(ii) From P and Q cut the bisector of ∠P and ∠Q, which intersect each other at point O.
(iii) With P as a center draw an in a circle that touches all the three sides of ∆RPQ.
APPEARS IN
RELATED QUESTIONS
Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO~Δ ABC.

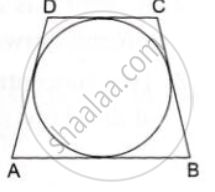
In the given figure, a circle touches all the four sides of a quadrilateral ABCD whose three sides are AB = 6cm, BC=7cm and CD=4 cm. Find AD.
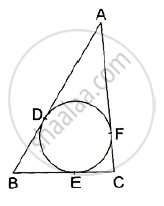
In the given figure, a cradle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14cm, BC = 8cm and CA=12 cm. Find the length AD, BE and CF.
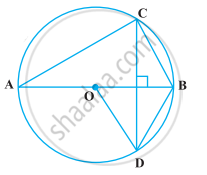
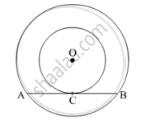
In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
Number of circles that can be drawn through three non-collinear points is
In the given figure, the area enclosed between the two concentric circles is 770 cm2. If the radius of the outer circle is 21 cm, calculate the radius of the inner circle.
If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is ______.
In the following figure, ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.

In the following figure, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.