Advertisements
Advertisements
Question
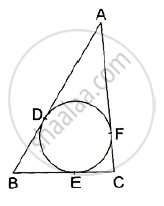
In the given figure, a cradle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14cm, BC = 8cm and CA=12 cm. Find the length AD, BE and CF.
Solution
We know that tangent segments to a circle from the same external point are congruent
Now, we nave
AD = AF,BD = BE and CE = CF
Now AD + BD = 14cm …..(1)
AF + FC = 12cm
⇒ AD + FC = 12cm .........(2)
BE + EC = 8cm
⇒ BD + FC= 8 cm ...........(3)
Adding all these we get
AD + BD + AD +FC +BD+ FC = 342
⇒ 2(AD + BD + FC) = 34
⇒ AD+ BO+ FC = 17cm ............(4)
Solving (1) and (4), we get
FC = 3cm
Solving (2) and (4), we get
BD = 5cm = BE
Solving (3) and (4), we get
and AD = 9cm
APPEARS IN
RELATED QUESTIONS
ABCD is a quadrilateral such that ∠D = 90°. A circle (O, r) touches the sides AB, BC, CD and DA at P,Q,R and If BC = 38 cm, CD = 25 cm and BP = 27 cm, find r.
A point P is 26 cm away from O of circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
Fill in the blank:
A point whose distance from the centre of a circle is greater than its radius lies in ..................... of the circle.
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

In the given figure ABC is an isosceles triangle and O is the centre of its circumcircle. Prove that AP bisects angle BPC .
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC ?
A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm2, find the sides PQ and PR.
Find the diameter of the circle
Radius = 8 cm
Draw any circle and mark
- it's centre
- a radius
- a diameter
- a sector
- a segment
- a point in its interior
- a point in its exterior
- an arc
