Advertisements
Advertisements
Question
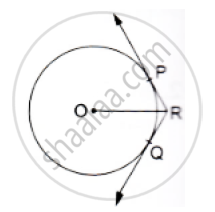
In the given figure, two tangents RQ, and RP and RP are drawn from an external point R to the circle with centre O. If ∠PRQ =120° , then prove that OR = PR + RQ.
Solution

Construction Join PO and OQ
In ΔPOR and ΔQOR
OP = OQ(Radii)
RP = RQ(Tangents from the external point are congruent)
OR = OR (Common)
By SSS congruency, ΔPOR ≅ ΔQOR
∠PRO = ∠QRO(C.P.C.T)
Now,∠PRO+ ∠QRO= ∠PRQ
⇒ 2 ∠PRO = 120°
⇒ ∠PRO = 60°
Now. In ΔPOR
cos 60° `=(PR)/(OR)`
⇒ `1/2 =(PR)/(OR)`
⇒ OR = 2PR
⇒ OR = PR + PR
⇒ OR = PR +RQ
APPEARS IN
RELATED QUESTIONS
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
From an external point P, tangents PA and PB are drawn to the circle with centre O. If CD is the tangent to the circle at point E and PA = 14 cm. Find the perimeter of ABCD.
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BC and DC into which BC is divided by the point of contact D, are of
lengths 6cm and 9cm respectively. If the area of 2 ΔABC = 54cm2 then find the lengths of sides AB and AC.

In Fig. 1, the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is ?
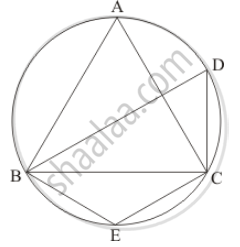
In the given figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.
ABC is a triangle with B as right angle, AC = 5 cm and AB = 4 cm. A circle is drawn with Aas centre and AC as radius. The length of the chord of this circle passing through C and B is
Construct a triangle PQR with QR = 5.5 cm, ∠Q = 60° and angle R = 45°. Construct the circumcircle cif the triangle PQR.
In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?
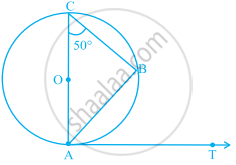
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at point A, then ∠BAT is equal to ______.
Is every diameter of a circle also a chord?
