Advertisements
Advertisements
Questions
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Prove that the perpendicular at the point of contact to a circle passes through the centre of the circle.
Solution 1
Let us consider a circle with centre O. Let AB be a tangent which touches the circle at P.
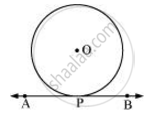
We have to prove that the line perpendicular to AB at P passes through centre O. We shall prove this by contradiction method.
Let us assume that the perpendicular to AB at P does not pass through centre O. Let it pass through another point O’. Join OP and O’P.
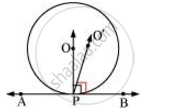
As perpendicular to AB at P passes through O’, therefore,
∠OPB = 90° … (1)
O is the centre of the circle and P is the point of contact. We know the line joining the centre and the point of contact to the tangent of the circle are perpendicular to each other.
∴ ∠OPB = 90° … (2)
Comparing equations (1) and (2), we obtain
∠OPB = ∠OPB … (3)
From the figure, it can be observed that,
∠OPB < ∠OPB … (4)
Therefore, ∠O’PB = ∠OPB is not possible. It is only possible, when the line O’P coincides with OP.
Therefore, the perpendicular to AB through P passes through centre O.
Solution 2
Let O be the centre of the circle.

A tangent PR has been drawn, touching the circle at point P.
Draw QP ⊥ RP at point P, such that Q lies on the circle.
∠OPR = 90° ...(Radius ⊥ tangent)
Also, ∠QPR = 90° ...(Given)
∴ ∠OPR = ∠QPR
Now, the above case is possible only when centre O lies on the line QP.
Hence, perpendicular at the point of contact to the tangent to a circle passes through the centre of the circle.
APPEARS IN
RELATED QUESTIONS
Prove that the lengths of the tangents drawn from an external point to a circle are equal.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
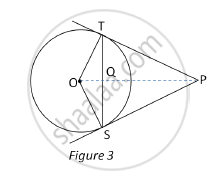
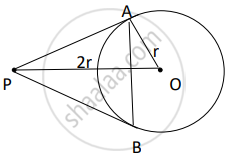
In Fig.3, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠ OTS = ∠ OST = 30°.
From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB.
Prove that a parallelogram circumscribing a circle is a rhombus.
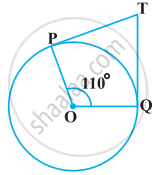
In the given figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to ______.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
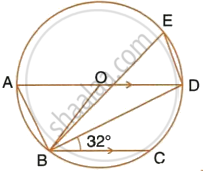
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
Find:
- ∠OBD
- ∠AOB
- ∠BED
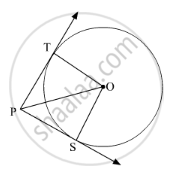
In Fig. 2, from a point P, two tangents PT and PS are drawn to a circle with centre O such that ∠SPT = 120°, Prove that OP = 2PS ?
Two concentric circles are of radii 5 cm and 3 cm. Length of the chord of the larger circle, (in cm), which touches the smaller circle is
(A) 4
(B) 5
(C) 8
(D) 10
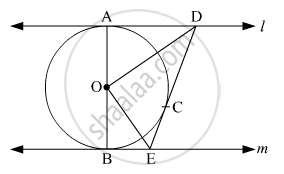
In fig. 6, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that ∠DOE = 90° ?
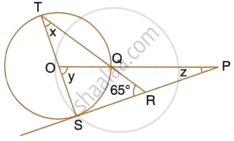
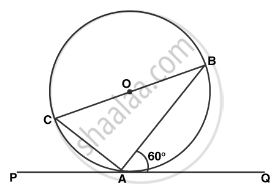
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and Z.
In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.
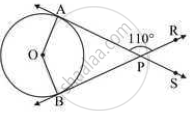
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 110°.
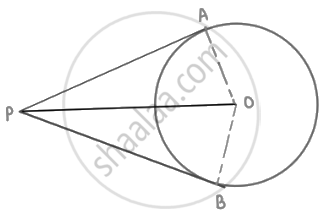
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
A tangent is drawn from a point at a distance of 17 cm of circle C(0, r) of radius 8 cm. The length of its tangent is ______
The length of tangents drawn from an external point to the circle ______
In the given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is ______

The length of the tangent from an external point P on a circle with centre O is ______
The length of the tangent from an external point on a circle is ______
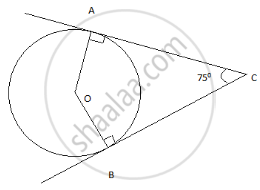
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB = ______
PA and PB are the two tangents drawn to the circle. O is the centre of the circle. A and B are the points of contact of the tangents PA and PB with the circle. If ∠OPA = 35°, then ∠POB = ______
In the given figure, PAQ is the tangent. BC is the diameter of the circle. ∠BAQ = 60°, find ∠ABC.
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = `asqrt(2)`.
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO, i.e., BO = 2BC.
In figure, common tangents AB and CD to two circles intersect at E. Prove that AB = CD.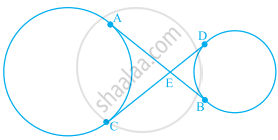
From a point P, two tangents PA and PB are drawn to a circle C(0, r). If OP = 2r, then find ∠APB. What type of triangle is APB?
In the given figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q meet at a point T. Find the length of TP.

Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
In the given figure, PA and PB are tangents from external point P to a circle with centre C and Q is any point on the circle. Then the measure of ∠AQB is ______.

Two concentric circles with centre O are of radii 3 cm and 5 cm. Find the length of chord AB of the larger circle which touches the smaller circle at P.

PA and PB are tangents drawn to the circle with centre O as shown in the figure. Prove that ∠APB = 2∠OAB.

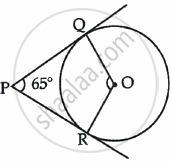
In the given figure, PQ and PR are tangents drawn from P to the circle with centre O such that ∠QPR = 65°. The measure of ∠QOR is ______.
In the given diagram, O is the centre of the circle. PR and PT are two tangents drawn from the external point P and touching the circle at Q and S respectively. MN is a diameter of the circle. Given ∠PQM = 42° and ∠PSM = 25°.
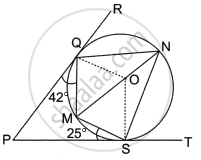
Find:
- ∠OQM
- ∠QNS
- ∠QOS
- ∠QMS
