Advertisements
Advertisements
Question
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = `asqrt(2)`.
Options
True
False
Solution
This statement is True.
Explanation:
Tangent is always perpendicular to the radius at the point of contact.
Hence, ∠RPT = 90°
If 2 tangents are drawn from an external point, then they are equally inclined to the line segment joining the centre to that point.
Consider the following figure,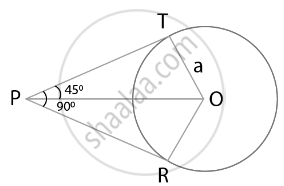
From point P, two tangents are drawn.
It is given that, OT = a
And line OP bisects ∠RPT.
So,
∠TPO = ∠RPO = 45°
We know that, OT ⊥ PT
In right-angled triangle OTP,
sin 45° = `"OT"/"OP"`
= `1/sqrt(2) = "a"/"OP"`
Hence, OP = `asqrt(2)`
APPEARS IN
RELATED QUESTIONS
In the below given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If∠PRQ = 120°, then prove that OR = PR + RQ.

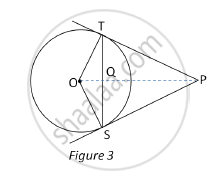
In Fig.3, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠ OTS = ∠ OST = 30°.
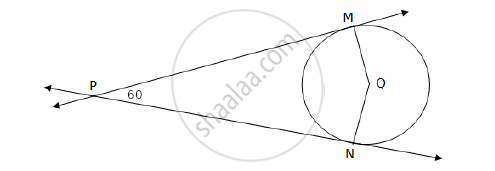
From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB.
Two concentric circles are of radii 5 cm and 3 cm. Length of the chord of the larger circle, (in cm), which touches the smaller circle is
(A) 4
(B) 5
(C) 8
(D) 10
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 60°, find ∠MQN.
Construct a pair of tangents to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.
In the given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is ______

Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the the perimeter of the triangle PCD.
