Advertisements
Advertisements
Question
In the below given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If∠PRQ = 120°, then prove that OR = PR + RQ.

Solution
Given that m∠PRQ = 120º

We know that the line joining the centre and the external point is the angle bisector between the tangents.
Thus, m∠PRO = m∠QRO =120º/2= 60º
Also we know that lengths of tangents from an external point are equal.
Thus, PR = RQ.
Join OP and OQ.
Since OP and OQ are the radii from the centre O,
OP ⊥ PR and OQ ⊥ RQ.
Thus, Δ OPR and ΔOQR are right angled congruent triangles.
Hence, ∠POR=90º- ∠PRO=90º - 60º= 30º
∠QOR=90°- ∠QRO=90° - 60° =30°
sin ∠QRO = sin30°=1/2
Thus,PR/OR=1/ 2
OR =2PR
OR =PR + PR
OR =PR + QR
APPEARS IN
RELATED QUESTIONS
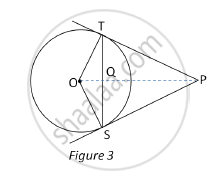
In Fig.3, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠ OTS = ∠ OST = 30°.
PQ is a tangent drawn from an external point P to a circle with centre O, QOR is the diameter of the circle. If ∠POR = 120°, what is the measure of ∠OPQ?
In fig. 6, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that ∠DOE = 90° ?
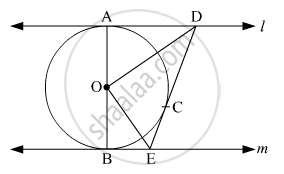
Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
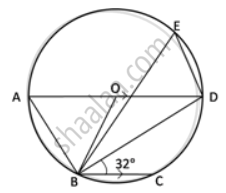
Find: ∠BED
If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm the length of each tangent is equal to ______
The number of tangents drawn at a point of the circle is/are ______
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
In the given figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q meet at a point T. Find the length of TP.

In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.

