Advertisements
Advertisements
Question
the below given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of ΔABC is 54 cm2, then find the lengths of sides AB and AC.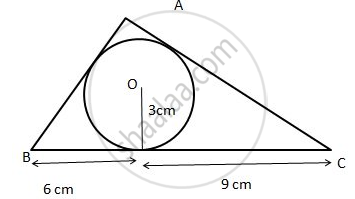
Solution
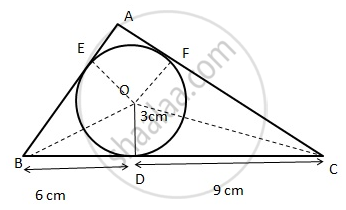
Given : OD = 3cm
Construction : Join OA, OB and X
Proof : Area of the ΔABC = area of ΔOBC + area of ΔOAC + arc of ∠ OAB.
BD = 6 cm : BE = 6 cm ( equal tangents )
DC = 9 cm : CF = 9 cm ( equal tangents )
AB = AF + FB = 6 + x = 6 + 3 = 9.
RELATED QUESTIONS
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

In the given figure,

AB || DC prove that
DM × BV = BM ✕ DU
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[BD = \frac{ac}{b + c}\]
In ∆ABC, ∠A = 60°. Prove that BC2 = AB2 + AC2 − AB . AC.
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
If the altitude of two similar triangles are in the ratio 2 : 3, what is the ratio of their areas?
If ∆ABC and ∆DEF are two triangles such that\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{3}{4}\], then write Area (∆ABC) : Area (∆DEF)
If D, E, F are the mid-points of sides BC, CA and AB respectively of ∆ABC, then the ratio of the areas of triangles DEF and ABC is
If in ∆ABC and ∆DEF, \[\frac{AB}{DE} = \frac{BC}{FD}\], then ∆ABC ∼ ∆DEF when
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
