Advertisements
Advertisements
Question
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
Options
AB2 − AD2 = BD.DC
AB2 − AD2 = BD2 − DC2
AB2 + AD2 = BD.DC
AB2 + AD2 = BD2 − DC2
Solution
Given: ΔABC is an isosceles triangle, D is a point on BC such that `AD ⊥ BC`
We know that in an isosceles triangle the perpendicular from the vertex bisects the base.
∴ BD = DC
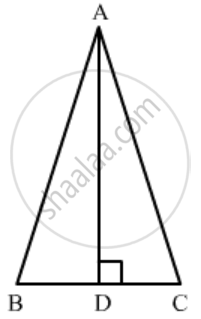
Applying Pythagoras theorem in ΔABD
`AB^2=AD^2+BD^2`
`⇒ AB^2-AD^2=BD^2`
`⇒ AB^2-AD^2=BDxxBD`
Since `BD =DC`
`⇒ AB^2-AD^2=BD xxDC`
Hence correct answer is `a`
APPEARS IN
RELATED QUESTIONS
Corresponding sides of two triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, determine the area of the larger triangle.
The diagonals of quadrilateral ABCD intersect at O. Prove that
`[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`
In the adjoining figure, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
If the altitude of two similar triangles are in the ratio 2 : 3, what is the ratio of their areas?
∆ABC and ∆BDE are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangle ABC and BDE is
In ∆ABC, D and E are points on side AB and AC respectively such that DE || BC and AD : DB = 3 : 1. If EA = 3.3 cm, then AC =
If D, E, F are the mid-points of sides BC, CA and AB respectively of ∆ABC, then the ratio of the areas of triangles DEF and ABC is
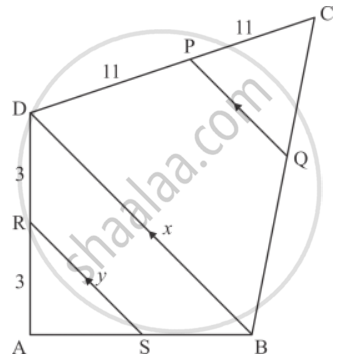
In the given figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively.
∆ABC is a right triangle right-angled at A and AD ⊥ BC. Then, \[\frac{BD}{DC} =\]
